Câu hỏi:
02/10/2024 190
1. Xác định hàm số \(y = ax + b\) để đồ thị của nó đi qua hai điểm \(A\left( {1;\,\, - 1} \right)\) và \(B\left( {4;\,\,5} \right)\).
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một ôtô dự định đi từ A đến B trong khoảng thời gian nhất định. Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi chậm mất so với dự định là 5 giờ. Tính vận tốc và thời gian dự định của ôtô.
1. Xác định hàm số \(y = ax + b\) để đồ thị của nó đi qua hai điểm \(A\left( {1;\,\, - 1} \right)\) và \(B\left( {4;\,\,5} \right)\).
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một ôtô dự định đi từ A đến B trong khoảng thời gian nhất định. Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi chậm mất so với dự định là 5 giờ. Tính vận tốc và thời gian dự định của ôtô.
Câu hỏi trong đề: Đề thi giữa kì 1 môn Toán lớp 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1. Vì đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A\left( {1;\,\, - 1} \right)\) và \(B\left( {4;\,\,5} \right)\) nên thay lần lượt từng cặp giá trị \(x,\,\,y\) vào hàm số, ta có: \(\left\{ \begin{array}{l} - 1 = a \cdot 1 + b\\5 = a \cdot 4 + b\end{array} \right.\) hay \(\left\{ \begin{array}{l}a + b = - 1\\4a + b = 5.\end{array} \right.\)
Trừ từng vế phương trình thứ hai cho phương trình thứ nhất của hệ phương trình trên, ta được:
\(3a = 6,\) suy ra \(a = 2.\)
Thay \(a = 2\) vào phương trình \(a + b = - 1,\) ta được:
\(2 + b = - 1,\) suy ra \(b = - 3.\)
Vậy hàm số cần tìm là \(y = 2x - 3.\)
2. Gọi \(x\) (km/h) là vận tốc dự định của ôtô và \(y\) (giờ) là thời gian dự định của ôtô để đi hết quãng đường AB \(\left( {x > 10,\,\,y > 0} \right).\)
– Quãng đường AB là \(xy\) (km).
– Nếu ôtô chạy nhanh hơn 10 km/h mỗi giờ thì đến nơi sớm hơn so với dự định là 3 giờ. Khi đó, ta có:
⦁ Vận tốc của ôtô lúc này là: \(x + 10\) (km/h).
⦁ Thời gian ôtô đi hết quãng đường AB là: \(y - 3\) (giờ).
⦁ Quãng đường AB là: \(\left( {x + 10} \right)\left( {y - 3} \right)\) (giờ).
Ta có phương trình: \(\left( {x + 10} \right)\left( {y - 3} \right) = xy\)
\(xy - 3x + 10y - 30 = xy\)
\( - 3x + 10y = 30\) (1)
– Nếu ôtô chạy chậm hơn 10 km/h mỗi giờ thì đến nơi muộn hơn so với dự định là 5 giờ. Khi đó, ta có:
⦁ Vận tốc của ôtô lúc này là: \(x - 10\) (km/h).
⦁ Thời gian ôtô đi hết quãng đường AB là: \(y + 5\) (giờ).
⦁ Quãng đường AB là: \(\left( {x + 10} \right)\left( {y + 5} \right)\) (giờ).
Ta có phương trình: \[\left( {x - 10} \right)\left( {y + 5} \right) = xy\]
\(xy + 5x - 10y - 50 = xy\)
\(5x - 10y = 50\) (2)
Từ phương trình (1) và phương trình (2) ta có hệ phương trình: \(\left\{ \begin{array}{l} - 3x + 10y = 30\\5x - 10y = 50\end{array} \right.\)
Cộng từng vế hai phương trình của hệ, ta được: \(2x = 80,\) suy ra \[x = 40\] (thỏa mãn).
Thay \[x = 40\] vào phương trình (1), ta được:
\( - 3 \cdot 40 + 10y = 30\) hay \(10y = 150,\) suy ra \(y = 15\) (thỏa mãn).
Vậy vận tốc dự định của ôtô là 40 (km/h) và thời gian ôtô đi hết quãng đường AB là 15 (giờ).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
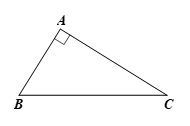
Tam giác \[ABC\] vuông tại \[A\], ta có: \[\sin \widehat {ABC} = \frac{{AC}}{{BC}}\].
Vậy ta chọn phương án A.Lời giải
Đáp án đúng là: D
Điều kiện xác định của phương trình \(\frac{1}{{x\left( {{x^2} + 4} \right)}} = \frac{{x + 1}}{x} - \frac{1}{{x - 2}}\) là \[x \ne 0\] và \[x - 2 \ne 0,\] hay \[x \ne 0\] và \[x \ne 2\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1