Câu hỏi:
13/10/2024 161Biết trong một trò chơi thể thao điện tử, có một chỉ số quan trọng là chỉ số DPS, biểu thị lượng sát thương gây ra mỗi giây. Lượng DPS trung bình của mỗi trận của hai xạ thủ A và B được thống kê qua 32 trận đấu tập luyện như sau:
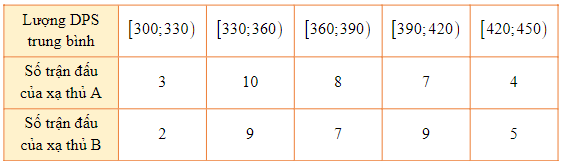
Khi đó:
a) Nếu xét về khoảng biến thiên thì lượng DPS trung bình của hai xạ thủ đồng đều nhau.
b) Biết giá trị trung bình sau 32 trận đấu tập của lượng DPS trung bình mỗi trận của mỗi xạ thủ trên 380 là đạt yêu cầu tập luyện. Vậy cả 2 xạ thủ trên đều đạt yêu cầu tập luyện.
c) Số trận đấu có lượng DPS trung bình mỗi trận dưới 360 của hai xạ thủ bằng nhau.
d) Nếu xét theo độ lệch chuẩn thì lượng DPS trung bình của xạ thủ A đồng đều hơn xạ thủ B.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
a) Khoảng biến thiên của mẫu số liệu của xạ thủ A là:
\({R_A} = 450 - 300 = 150.\)
Khoảng biến thiên của mẫu số liệu của xạ thủ B là:
\({R_B} = 450 - 300 = 150.\)
Do đó, nếu xét về khoảng biến thiên thì lượng DPS trung bình của hai xạ thủ đồng đều nhau.
Vậy ý a đúng
b) Tính giá trị trung bình của mẫu số liệu trên, ta được:
\(\overline {{x_A}} = \frac{{315.3 + 345.10 + 375.8 + 405.7 + 435.4}}{{32}} = 374,0625.\)
\(\overline {{x_B}} = \frac{{315.2 + 345.9 + 375.7 + 405.9 + 435.5}}{{32}} = 380,625.\)
Theo đề, giá trị trung bình sau 32 trận đấu tập của lượng DPS trung bình mỗi trận của mỗi xạ thủ trên 380 là đạt yêu cầu tập luyện. Do đó chỉ xạ thủ B đạt yêu cầu.
Vậy ý b sai.
c) Số trận đấu có lượng DPS trung bình mỗi trận dưới 360 của xạ thủ A là:
\(3 + 10 = 13\) (trận).
Số trận đấu có lượng DPS trung bình mỗi trận dưới 360 của xạ thủ B là:
\(2 + 9 = 11\) (trận).
Vậy ý c sai.
d) Độ lệch chuẩn của mẫu số liệu của xạ thủ A là:
\({s_A} = \sqrt {\frac{{{{315}^2}.3 + {{345}^2}.10 + {{375}^2}.8 + {{405}^2}.7 + {{435}^2}.4}}{{32}} - 374,{{0625}^2}} \approx 35,56.\)
Độ lệch chuẩn của mẫu số liệu của xạ thủ B là:
\({s_B} = \sqrt {\frac{{{{315}^2}.2 + {{345}^2}.9 + 375.7 + {{405}^2}.9 + {{435}^2}.5}}{{32}} - 380,{{625}^2}} \approx 35,53.\)
Nhận thấy \({s_B} < {s_A}\) nên nếu xét theo độ lệch chuẩn thì lượng DPS trung bình của xạ thủ B đồng đều hơn xạ thủ A.
Vậy d sai.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
Mẫu số liệu ghép nhóm có phương sai \[{s^2} = 25\] thì độ lệch chuẩn \(s = \sqrt {{s^2}} = \sqrt {25} = 5\).
Lời giải
Đáp án đúng là: C
a) Ta có:
Số học sinh lớp 12A là: \({n_A} = 2 + 16 + 9 + 6 + 3 = 36\) (học sinh).
Số học sinh lớp 12B là: \({n_B} = 0 + 15 + 13 + 4 + 6 = 38\) (học sinh).
Do đó sĩ số lớp 12B nhiều hơn lớp 12A.
Vậy ý a sai.
b) Điểm kiểm tra trung bình lớp 12A là:
\({\overline x _A} = \frac{{2.3,25 + 16.4,75 + 9.6,26 + 6.7,75 + 3.9,25}}{{36}} = \frac{{71}}{{12}}.\)
Điểm kiểm tra trung bình lớp 12B là:
\({\overline x _B} = \frac{{15.4,75 + 13.6,25 + 4.7,75 + 6.9,25}}{{38}} = \frac{{239}}{{38}}\).
Sự chênh lệch giữa điểm kiểm tra trung bình của hai lớp là:
\(\frac{{239}}{{38}} - \frac{{71}}{{12}} \approx 0,373.\)
Vậy điểm kiểm tra trung bình của hai lớp chênh lệch nhau không quá 0,5 điểm.
Vậy ý b đúng.
c) Khoảng biến thiên của số liệu lớp 12A là: \({R_A} = 10 - 2,5 = 7,5\) (điểm).
Khoảng biến thiên của số liệu lớp 12B là: \({R_B} = 10 - 4 = 6\) (điểm).
Nếu xét theo khoảng biến thiên thì điểm kiểm tra của lớp 12B đồng đều hơn do \({R_A} > {R_B}\).
Do đó ý c đúng.
d) Độ lệch chuẩn của mẫu số liệu lớp 12A là:
\({s_A} = \sqrt {\frac{{2.3,{{25}^2} + 16.4,{{75}^2} + 9.6,{{25}^2} + 6.7,{{75}^2} + 3.9,{{25}^2}}}{{36}} - {{\left( {\frac{{71}}{{12}}} \right)}^2}} \approx 1,586.\)
Độ lệch chuẩn của mẫu số liệu lớp 12B là:
\({s_B} = \sqrt {\frac{{15.4,{{75}^2} + 13.6,{{25}^2} + 4.7,{{75}^2} + 6.9,{{25}^2}}}{{38}} - {{\left( {\frac{{239}}{{38}}} \right)}^2}} \approx 1,595.\)
Thấy \({s_B} > {s_A}\) nên nếu xét theo độ lệch chuẩn thì điểm kiểm tra của lớp 12A lại đồng đều hơn.
Vậy ý d đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)