Câu hỏi:
16/10/2024 5,549Trong không gian \[Oxyz\], cho mặt cầu \[\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\] và hình nón \[\left( H \right)\] có đỉnh \[A\left( {3;2; - 2} \right)\] và nhận \[AI\] là trục đối xứng với \[I\] là tâm mặt cầu. Một đường sinh hình nón \[\left( H \right)\] cắt mặt cầu tại \[M,N\]sao cho \[AM = 3AN\]. Viết phương trình mặt cầu đồng tâm với mặt cầu \[\left( S \right)\], tiếp xúc với các đường sinh của hình nón \[\left( H \right).\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
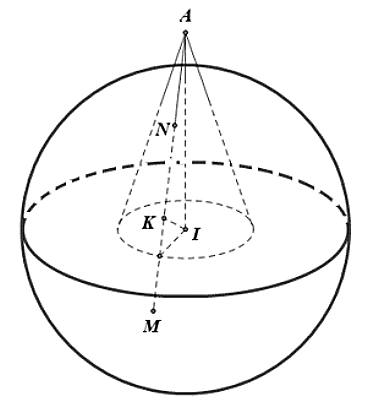
Gọi hình chiếu vuông góc của
\[I\] trên \[MN\] là \[K\].
Dễ thấy \[AN = NK = \frac{1}{3}AM\], mặt cầu \[\left( S \right)\] có tâm \[I\left( {1;2;3} \right)\] và bán kính \[R = 5.\]
Có \[AM.AN = A{I^2} - {R^2} = 4\]\[ \Rightarrow A{N^2} = \frac{4}{3}\]
\[ \Rightarrow AN = NK = \frac{{2\sqrt 3 }}{3}\]\[ \Rightarrow IK = \sqrt {I{N^2} - K{N^2}} = \frac{{\sqrt {213} }}{3}.\]
Nhận thấy mặt cầu đồng tâm với mặt cầu \[\left( S \right)\] và tiếp xúc với các đường sinh của hình nón \[\left( H \right)\] chính là mặt cầu tâm \[I\left( {1;2;3} \right)\], bán kính \[IK = \frac{{\sqrt {213} }}{3}.\]
Vậy phương trình mặt cầu cần tìm là: \[{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{71}}{3}.\]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
Gọi \[A\left( {a;0;0} \right),B\left( {0;b;0} \right),C\left( {0;0;c} \right)\].
Tam giác \[ABC\] có trọng tâm \[G\left( { - 6; - 12;18} \right)\] nên ta có:
\[\left\{ \begin{array}{l}\frac{{a + 0 + 0}}{3} = - 6\\\frac{{0 + b + 0}}{3} = - 12\\\frac{{0 + 0 + c}}{3} = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 18\\b = - 36\\c = 54\end{array} \right.\].
Suy ra \[A\left( { - 18;0;0} \right),B\left( {0; - 36;0} \right),C\left( {0;0;54} \right)\].
Gọi \[I\left( {x;y;z} \right)\], ta có: \[\left\{ \begin{array}{l}IO = IA\\IA = IB\\IB = IC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}I{O^2} = I{A^2}\\I{A^2} = I{B^2}\\I{B^2} = I{C^2}\end{array} \right.\].
\[ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} + {z^2} = {\left( {x + 18} \right)^2} + {y^2} + {z^2}\\{\left( {x + 18} \right)^2} + {y^2} + {z^2} = {x^2} + {\left( {y + 36} \right)^2} + {z^2}\\{x^2} + {\left( {y + 36} \right)^2} + {z^2} = {x^2} + {y^2} + {\left( {z - 54} \right)^2}\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}36x + 324 = 0\\36x + 324 - 72y - 1296 = 0\\72y + 1296 + 108z - 2916 = 0\end{array} \right.\]
\[ \Leftrightarrow \left\{ \begin{array}{l}x = - 9\\y = - 18\\z = 27\end{array} \right.\].
Vậy tâm của mặt cầu là \[I\left( { - 9; - 18;27} \right).\]
Lời giải
Đáp án đúng là: D
Xét các đáp án như sau:
• Với \[{x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\] ta có: \[a = - 1,b = - 1,c = 1,d = 4\].
Suy ra \[{a^2} + {b^2} + {c^2} - d = - 1 < 0.\]
Vậy đáp án A không là phương trình mặt cầu.
• Với \[{x^2} + {y^2} + {z^2} + 4x - 2y + 2z + 6 = 0\] ta có: \[a = - 2,b = 1,c = - 1,d = 6\].
Suy ra \[{a^2} + {b^2} + {c^2} - d = 0\]
Vậy đáp án B không là phương trình mặt cầu.
• Với \[{x^2} + {y^2} + {z^2} + 2x - 6y + 4z + 14 = 0\] có: \[a = - 1,b = 3,c = - 2,d = 14\].
Suy ra \[{a^2} + {b^2} + {c^2} - d = 0\]
Vậy đáp án C không là phương trình mặt cầu.
• Với \[{x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\] có: \[a = - 4,b = 3,c = - 1,d = - 10\].
Suy ra \[{a^2} + {b^2} + {c^2} - d = 36 > 0.\]
Vậy đáp án D là phương trình của một mặt cầu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
Nhắn tin Zalo