Câu hỏi:
22/10/2024 1,215
Với hình vuông A1B1C1D1 như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy định sau:
Bước 1: Tô màu "đẹp" cho hình vuông A1B1C1D1.
Bước 2: Tô màu "đẹp" cho hình vuông A2B2C2D2 là hình vuông ở chính giữa khi chia hình vuông A1B1C1D1 thành 9 phần bằng nhau như hình vẽ.
Bước 3: Tô màu "đẹp" cho hình vuông A3B3C3D3 là hình vuông ở chính giữa khi chia hình vuông A2B2C2D2 thành 9 phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần đúng bao nhiêu bước để tổng diện tích phần được tô màu chiếm \(\frac{{40}}{{81}}\) phần diện tích hình vuông ban đầu?
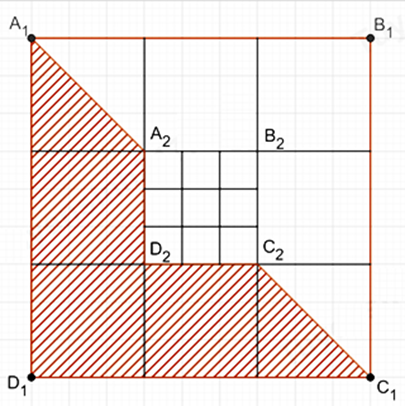
Với hình vuông A1B1C1D1 như hình vẽ bên, cách tô màu như phần gạch sọc được gọi là cách tô màu “đẹp”. Một nhà thiết kế tiến hành tô màu cho một hình vuông như hình bên, theo quy định sau:
Bước 1: Tô màu "đẹp" cho hình vuông A1B1C1D1.
Bước 2: Tô màu "đẹp" cho hình vuông A2B2C2D2 là hình vuông ở chính giữa khi chia hình vuông A1B1C1D1 thành 9 phần bằng nhau như hình vẽ.
Bước 3: Tô màu "đẹp" cho hình vuông A3B3C3D3 là hình vuông ở chính giữa khi chia hình vuông A2B2C2D2 thành 9 phần bằng nhau. Cứ tiếp tục như vậy. Hỏi cần đúng bao nhiêu bước để tổng diện tích phần được tô màu chiếm \(\frac{{40}}{{81}}\) phần diện tích hình vuông ban đầu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp giải
Lời giải
Gọi diện tích được tô màu ở mỗi bước là \({u_n},n \in {\mathbb{N}^*}\). Dễ thấy dãy các giá trị \({u_n}\) là một cấp số nhân với số hạng đầu \({u_1} = \frac{4}{9}\) và công bội \(q = \frac{1}{9}\).
Gọi \({S_k}\) là tổng của \(k\) số hạng đầu trong cấp số nhân đang xét thì \({S_k} = \frac{{{u_1}\left( {{q^k} - 1} \right)}}{{q - 1}}\). Để tổng diện tích phần được tô màu chiếm \(\frac{{40}}{{81}}\) phần diện tích hình vuông ban đầu thì \(\frac{{{u_1}\left( {{q^k} - 1} \right)}}{{q - 1}} = \frac{{40}}{{81}} \Leftrightarrow k = 2\).
Vậy cần đúng 2 bước.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải
Cấp số cộng
Lời giải
Ta có chiều dài của mỗi mặt cầu thang theo thứ tự lập thành một cấp số cộng với số hạng đầu tiên là \({u_1} = 189\), công sai \(d = - 7\) và số hạng cuối cùng là \({u_n} = 63\).
Khi đó áp dụng công thức tính số hạng tồng quát ta có:
\({u_n} = {u_1} + (n - 1)d \Leftrightarrow 63 = 189 - 7(n - 1) \Leftrightarrow n = 19\)
Tổng chiều dài của 19 hình chữ nhật đó là: .
Diện tích của 19 bậc thang là:
Tổng số tiền để làm cầu thang đó là: đồng.\({S_{19}} = 19.\frac{{{u_1} + {u_{19}}}}{2} = 2394\)
Lời giải
Phương pháp giải
Lời giải
Gọi số cần tìm có dạng \[m = \overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \] với \({a_i} \in \{ 0;1;2;3;4;5;6;7;8;9\} ,\,\,{a_1} \ne 0\) và \(i \in \{ 1;2;3;4;5;6\} \).
Vì các chữ số \({a_1},{a_2},{a_3},{a_4},{a_5},{a_6}\) là đôi một khác nhau, có nhiều hơn một chữ số lẻ và đồng thời trong đó có hai chữ số kề nhau không cùng là số lẻ nên ta xét hai trường hợp sau:
1. Trường hợp 1. Có 4 chữ số chẵn và 2 chữ số lẻ.
- Chữ số 0 đứng ở vị trí bất kì.
- Lấy 4 chữ số chẵn và 2 chữ số lẻ có \(C_5^4.C_5^2\).
- Xếp 4 chữ số chẵn có 4!.
- Xếp 2 chữ số lẻ có \(A_5^2\).
Vậy trường hợp này có \(C_5^4.C_5^2.4!.A_5^2 = 24000\) số.
- Chữ số a1 = 0.
- Lấy thêm 3 chữ số chẵn; 2 chữ số lẻ có \(C_4^3.C_5^2\).
- Xếp 3 chữ số chẵn có 3!.
- Xếp 2 chữ số lẻ có \(A_4^2\).
Vậy trường hợp này có \(C_4^3.C_5^2.3!.A_4^2 = 2880\).
2. Trường hợp 2 . Có 3 chữ số chẵn và 3 chữ số lẻ.
- Chữ số 0 dứng ở vị trí bất kì.
- Lấy 3 chữ số chẵn và 3 chữ số lẻ có \(C_5^3.C_5^3\).
- Xếp 3 chữ số chẵn có 3!.
- Xếp 3 chữ số lẻ có \(A_4^3\).
Vậy trường hợp này có \(C_5^3.C_5^3.3!.A_4^3 = 14400\) số.
- Chữ số a1 = 0.
- Lấy thêm 2 chữ số chẵn; 3 chữ số lẻ có \(C_4^2.C_5^3\).
- Xếp 2 chữ số chẵn có 2!.
- Xếp 3 chữ số lẻ có \(A_3^3 = 3!\).
Vậy trường hợp này có \(C_4^2.C_5^3.2!.3! = 720\).
Vậy có (24000 − 2880) + (14400 − 720) = 34800 số thỏa mãn yêu cầu bài toán.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận