Gọi \(E\) là tập hợp tất cả các số nguyên dương \(y\) sao cho ứng với mỗi số \(y\) có không quá 4031 số nguyên \(x\) thỏa mãn \({\rm{log}}_2^2x - 3y{\rm{lo}}{{\rm{g}}_2}x + 2{y^2} < 0\). Tập \(E\) có bao nhiêu phần tử?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giải thích
Điều kiện \(x > 0\).
Đặt \(t = {\rm{lo}}{{\rm{g}}_2}x\), bất phương trình trở thành \({t^2} - 3yt + 2{y^2} < 0\,\,\left( * \right)\).
\({\rm{\Delta }} = {(3y)^2} - 4.2{y^2} = {y^2} > 0,\forall y \in {\mathbb{Z}^ + }\), tam thức có hai nghiệm \(\left[ {\begin{array}{*{20}{l}}{t = y}\\{t = 2y}\end{array}} \right.\).
Do đó \(\left( * \right) \Leftrightarrow y < t < 2y\) hay \(y < {\rm{lo}}{{\rm{g}}_2}x < 2y \Leftrightarrow {2^y} < x < {2^{2y}}\).
Vì \(x,y \in {\mathbb{Z}^ + }\)nên \(x \in A = \left\{ {{2^y} + 1;{2^y} + 2; \ldots ;{2^{2y}} - 1} \right\}\).
Số phần tử của tập \(A\) là \(\left( {{2^{2y}} - 1} \right) - \left( {{2^y} + 1} \right) + 1 = {2^{2y}} - {2^y} - 1\).
Giả thiết bài toán có không quá 4031 số nguyên \(x\) nên ta có. \({2^{2y}} - {2^y} - 1 \le 4031\)
\( \Leftrightarrow {2^{2y}} - {2^y} - 4032 \le 0 \Leftrightarrow - 63 \le {2^y} \le 64 \Leftrightarrow y \le 6\).
Vì \(y \in {\mathbb{Z}^ + }\)nên \(y \in E = \left\{ {1;2;3;4;5;6} \right\}\).
Số phần tử của tập hợp \(E\) là 6 .
Chọn A
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án
|
Mệnh đề |
Đúng |
Sai |
|
1) Đồ thị hàm số có một tiệm cận ngang là \(y = - 1\). |
X | |
|
2) Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 2. |
X |
Giải thích
|
Lí do lựa chọn phương án |
1 |
Đúng vì: Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 3x + 2}}{{1 - {x^2}}} = - 1\) nên đồ thị hàm số có một tiệm cận ngang \(y = - 1\). |
|
2 |
Đúng vì: Ta có: \(\mathop {\lim }\limits_{x \to 1} y = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{1 - {x^2}}} = \mathop {\lim }\limits_{x \to 1} \frac{{2 - x}}{{x + 1}} = \frac{1}{2}\) nên \(x = 1\) không là tiệm cận đứng của đồ thị hàm số. \(\mathop {\lim }\limits_{x \to {{( - 1)}^ + }} y = \mathop {\lim }\limits_{x \to {{( - 1)}^ + }} \frac{{{x^2} - 3x + 2}}{{1 - {x^2}}} = \mathop {\lim }\limits_{x \to {{( - 1)}^ + }} \frac{{2 - x}}{{x + 1}} = + \infty {\rm{. }}\) Khi đó, đồ thị hàm số có một tiệm cận đứng \(x = - 1\). |
Lời giải
Đáp án
|
Phát biểu |
Đúng |
Sai |
|
Diện tích khu đất lớn nhất khi độ dài hàng rào \(AD\) là 125 mét. |
X | |
|
Diện tích khu đất lớn nhất khi chi phí nguyên vật liệu làm hàng rào \(AB\) là 7 triệu đồng. |
X | |
|
Diện tích khu đất lớn nhất bằng \(5200{\rm{\;}}{{\rm{m}}^2}\). |
X |
Giải thích
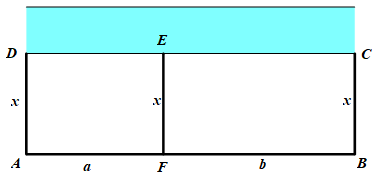
Gọi chiều rộng của hình chữ nhật là \(x\left( m \right){\rm{\;}}(x > 0)\) và chiều dài của phần đất trồng rau và nuôi gà lần lượt là \(a\left( m \right),b\left( m \right){\rm{\;}}(a > 0;b > 0)\).
Khi đó diện tích của khu đất là \(S = \left( {a + b} \right)x\left( {{m^2}} \right)\).
Mặt khác theo giả thiết tổng chi phí là 20 triệu đồng nên ta có:
\(3x.40000 + \left( {a + b} \right)80000 = 20000000 \Leftrightarrow 3x + 2\left( {a + b} \right) = 500\).
Ta có \(6S = 3x.2\left( {a + b} \right) \le \frac{{{{[3x + 2\left( {a + b} \right)]}^2}}}{4} = \frac{{{{500}^2}}}{4} \Rightarrow S \le \frac{{31250}}{3}\).
\( \Rightarrow {{\rm{S}}_{{\rm{max}}}} = \frac{{31250}}{3} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{a + b = 125}\\{x = \frac{{250}}{3}\,\,\,}\end{array}} \right.\)
\( \Rightarrow \) Chi phí nguyên vật liệu làm hàng rào \(AB\) là: \(125.80000 = 10000000\) (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo