Cho đường tròn \[\left( {O;OA} \right)\] và đường tròn \[\left( {O'} \right)\] đường kính \[OA.\] Vị trí tương đối của hai đường tròn\[\left( O \right)\] và \[\left( {O'} \right)\] là
A. Tiếp xúc trong.
Quảng cáo
Trả lời:
Đáp án đúng là: A

Vì đường tròn \[\left( {O'} \right)\] có đường kính \[OA\] nên \[O'\] là trung điểm \[OA.\]
Do đó \[OO' = O'A = \frac{{OA}}{2}.\]
Đặt \[R = OA\] và \[R' = O'A = \frac{{OA}}{2}.\] Suy ra \[R > R'.\]
Ta có \[OA - \frac{{OA}}{2} = \frac{{OA}}{2}.\] Suy ra \[R - R' = OO',\] với \[R > R'.\]
Khi đó hai đường tròn \[\left( {O;OA} \right)\] và \[\left( {O';\frac{{OA}}{2}} \right)\] tiếp xúc trong.
Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Tam giác cân.
Lời giải
Đáp án đúng là: C
Vì \(AB\) và \(AC\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) cắt nhau tại \(A\) nên \(AO\) là tia phân giác của \(\widehat {BAC}.\) Do đó \[\widehat {BAO} = \frac{1}{2}\widehat {BAC} = \frac{1}{2} \cdot 90^\circ = 45^\circ .\]
Do \(AB\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B\) nên \(AB \bot OB\).
Khi đó \(\Delta ABO\) vuông tại \(B\) có \[\widehat {BAO} = 45^\circ \] nên là tam giác vuông cân tại \(B\).
Câu 2
A. \[\frac{{4\pi }}{3}{\rm{\;cm}}.\]
Lời giải
Đáp án đúng là: D

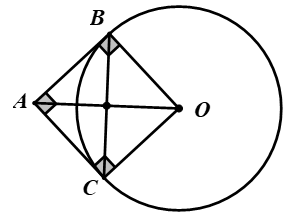
Ta có \(BC \bot OA\) tại trung điểm \[M\] của \[OA\] nên \(BC\) là đường trung trực của đoạn thẳng \(OA.\)
Do đó \[OB = AB.\]
Mà \[OA = OB\] nên \[OA = OB = AB.\] Suy ra tam giác \[OAB\] là tam giác đều.
Do đó \[\widehat {AOB} = 60^\circ .\]
Chứng minh tương tự, ta được \[\widehat {AOC} = 60^\circ .\]
Ta có
Khi đó số đo cung lớn \[BC\] bằng
Độ dài cung lớn \[BC\] là: \[l = \frac{n}{{360}}C = \frac{{240}}{{360}} \cdot 4\pi = \frac{{8\pi }}{3}{\rm{\;(cm)}}{\rm{.}}\]
Vậy ta chọn phương án D.
Câu 3
A. \[8,5{\rm{\;cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Chỉ (i) đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\frac{{25\pi }}{2}{\rm{\;d}}{{\rm{m}}^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\widehat {AOD} = 3\widehat {ACD}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[d \equiv OA.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một họa tiết trang trí có dạng hình tròn bán kính \[5{\rm{\;dm}}\] được chia thành nhiều hình quạt tròn (hình vẽ), mỗi hình quạt tròn có góc ở tâm là \[7,5^\circ .\] Diện tích tất cả các hình (ảnh 1)](https://video.vietjack.com/upload2/images/1731403622/1731404338-image12.png)