Tam giác \[ABC\] có 3 đỉnh nằm trên đường tròn \[\left( O \right)\] có \[AB = 5\,\,{\rm{cm}}\]; \[AC = 3\,\,{\rm{cm}}\]. Vẽ đường cao \[AH\] và đường kính \[AD\]. Khi đó tích \[AH.{\rm{ }}AD\] bằng
A. \(15\,\,{\rm{c}}{{\rm{m}}^2}\).
B. \(8\,\,{\rm{c}}{{\rm{m}}^2}\).
C. \(12\,\,{\rm{c}}{{\rm{m}}^2}\).
D. \(30\,\,{\rm{c}}{{\rm{m}}^2}\).
Quảng cáo
Trả lời:
Đáp án đúng là: A
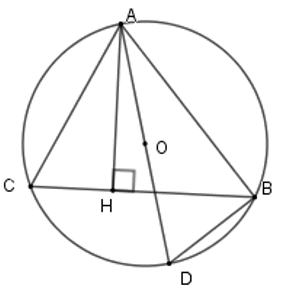
Xét \[\left( O \right)\] có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \[AB\]); \[\;\widehat {ADB} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn).
Nên ∆\[ACH\]ᔕ ∆\[ADB\] (g.g), do đó \(\frac{{AC}}{{AD}} = \frac{{AH}}{{AB}}\) hay \[AH.{\rm{ }}AD = AC.{\rm{ }}AB\].
Suy ra \[AH.{\rm{ }}AD = 3.5 = 15\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right).\]
Vậy \[AH.{\rm{ }}AD = 3 \cdot 5 = 15\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right).\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(30^\circ \).
B. \(45^\circ \).
C. \[60^\circ \].
D. \(90^\circ \).
Lời giải
Đáp án đúng là: C
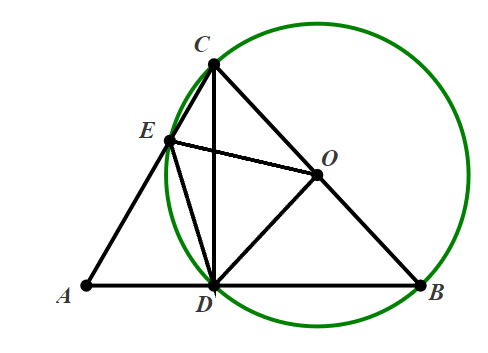
Góc \[BDC\] là góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \(\widehat {BDC} = 90^\circ \).
Suy ra \(\widehat {ADC} = 180^\circ - \widehat {BDC} = 180^\circ - 90^\circ = 90^\circ \) hay tam giác \[ADC\] vuông tại \[D\].
Suy ra \(\widehat {ACD} = 90^\circ - \widehat {CAD} = 90^\circ - 60^\circ = 30^\circ \).
Vì \[\widehat {EOD}\] và \[\widehat {ECD}\] là góc ở tâm và góc nội tiếp cùng chắn cung \[ED\] của \[\left( O \right)\] nên:
\(\widehat {EOD} = 2\widehat {ECD} = 2 \cdot 30^\circ = 60^\circ \).
Mà tam giác \[EOD\] cân tại \[O\], suy ra tam giác \[EOD\] là tam giác đều.
Vậy \(\widehat {EDO} = 60^\circ \).
Câu 2
A. \[BH = BE\].
B.\[BH = CF\].
C.\[BH = CH\].
D.\[HF = BC\].
Lời giải
Đáp án đúng là:
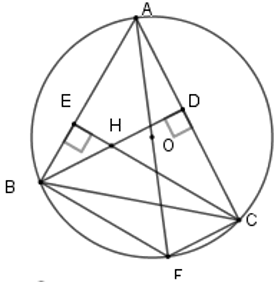
Xét \[\left( O \right)\] có \[\widehat {ACF} = 90^\circ \,;\,\,\widehat {ABF} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn).
Suy ra \[CF \bot \;AC\]; \[BF \bot \;AB\] mà \[BD \bot \;AC\]; \[CE \bot \;AB\], do đó \[BD\,{\rm{//}}\,CF\]; \[CE\,{\rm{//}}\,BF\].
Suy ra \[BHCF\] là hình bình hành hay \[BH = CF\].
Câu 3
A. \(50^\circ \).
B. \(60^\circ \).
C. \(45^\circ \).
D. \(70^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(90^\circ \).
B. \(80^\circ \).
C. \(110^\circ \).
D. \(120^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[ID \cdot CD\].
B. \[IC \cdot CB\].
C. \[IC \cdot CD\].
D. \[IC \cdot ID\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
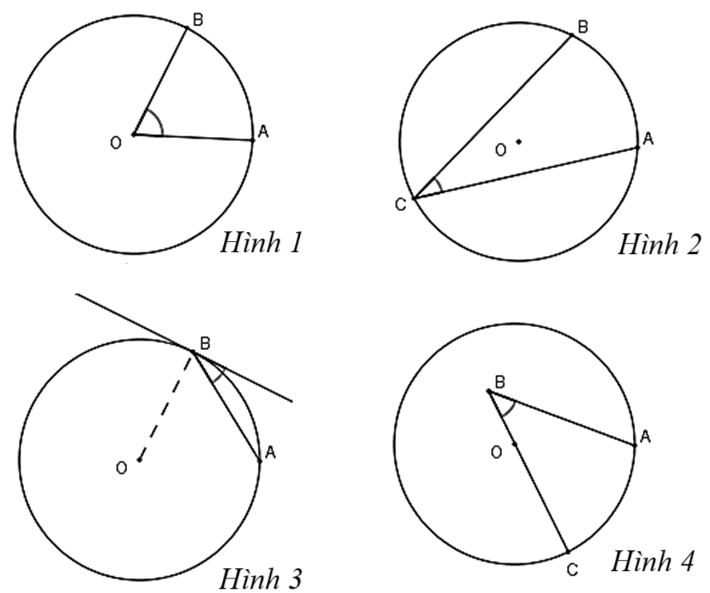
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.