Câu hỏi:
14/11/2024 221Phép quay giữ nguyên hình đa giác đều \[{A_1}{A_2}{A_3}...{A_n}\,\,\left( {n \ge 3,{\rm{ }}n \in \mathbb{N}} \right)\] là
Đáp án chính xác
Câu hỏi trong đề: 15 câu trắc nghiệm Toán 9 Cánh diều Ôn tập chương IX có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Giả sử hình đa giác đều \[{A_1}{A_2}{A_3}...{A_n}\,\,\left( {n \ge 3,{\rm{ }}n \in \mathbb{N}} \right)\] có tâm \[O.\]
Phép quay giữ nguyên hình đa giác đều \[{A_1}{A_2}{A_3}...{A_n}\] là phép quay tâm \[O\] biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đều đó.
Do đó phép quay giữ nguyên hình đa giác đều \[{A_1}{A_2}{A_3}...{A_n}\,\,\left( {n \ge 3,{\rm{ }}n \in \mathbb{N}} \right)\] là phép quay có tâm là tâm của hình đa giác đều biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đều đó.
Vậy ta chọn phương án C.
Nhà sách vietjack
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
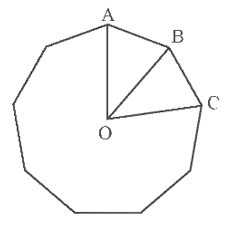
Câu 1:
Cho đa giác đều 9 cạnh có tâm \[O\] và \[AB,{\rm{ }}BC\] là hai cạnh của đa giác (như hình vẽ).
Số đo các góc \[\widehat {AOB}\,,\,\,\widehat {ABO}\,,\,\,\widehat {ABC}\] lần lượt là
Xem đáp án »
14/11/2024
2,935
Câu 2:
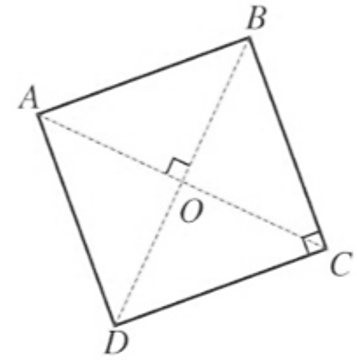
Cho hình vuông \[ABCD\] tâm \[O.\] Phép quay ngược chiều 180° tâm O biến các điểm \[A,\,\,B,\,\,C,\,\,D\] thành các điểm nào?
Xem đáp án »
14/11/2024
2,821
Câu 3:
Cho hình ngũ giác đều \[ABCDE\] tâm \[O\]. Các phép quay tâm \[O\] giữ nguyên hình ngũ giác đều là
Xem đáp án »
14/11/2024
1,716
Câu 4:
Phép quay với \[O\] là tâm biến tam giác đều thành chính nó là phép quay thuận chiều một góc
Xem đáp án »
14/11/2024
791
Câu 5:
Cho ngũ giác đều \[MNPQR\] có tâm \[O.\] Phép quay nào với tâm \[O\] biến ngũ giác đều \[MNPQR\] thành chính nó?
Xem đáp án »
14/11/2024
687
Câu 6:
Cho bát giác đều \[ABCDEFGH\] có tâm \[O.\] Phép quay thuận chiều \[135^\circ \] tâm \[O\] biến điểm \[D\] của bát giác đều \[ABCDEFGH\] thành điểm nào?
Xem đáp án »
14/11/2024
587
Câu 7:
III. Vận dụng
Cho lục giác đều \[ABCDEF\] tâm \[O.\] Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[EF,{\rm{ }}BD.\] Khẳng định nào sau đây là sai?
Xem đáp án »
14/11/2024
285
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 03
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận