Câu hỏi:
30/11/2024 172
Chiều dài của 40 bé sơ sinh 12 ngày tuổi được chọn ngẫu nhiên ở viện nhi trung ương được nghiên cứu thống kê ở bảng dưới đây:
Chiều dài (cm)
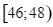
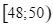
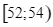
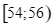
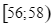
Số trẻ
3
3
10
15
7
2
Tìm phương sai ( làm tròn đến hàng phần trăm) của 40 bé sơ sinh ở bảng thống kê trên
Chiều dài của 40 bé sơ sinh 12 ngày tuổi được chọn ngẫu nhiên ở viện nhi trung ương được nghiên cứu thống kê ở bảng dưới đây:
|
Chiều dài (cm) |
|
|
|
|
|
|
|
Số trẻ |
3 |
3 |
10 |
15 |
7 |
2 |
Tìm phương sai ( làm tròn đến hàng phần trăm) của 40 bé sơ sinh ở bảng thống kê trên
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: 5,91
Ta có bảng phân bố của mẫu ghép nhóm 40 bé sơ sinh
|
Chiều dài (cm) |
|
|
|
|
|
|
|
Số trẻ |
3 |
3 |
10 |
15 |
7 |
2 |
|
Chiều dài đại diện (cm) |
45 |
47 |
49 |
51 |
53 |
55 |
Chiều dài trung bình của 40 trẻ là:
(cm).
Phương sai của 40 bé sơ sinh ở bảng thống kê trên là:
.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đ, b) S, c) S, d) Đ
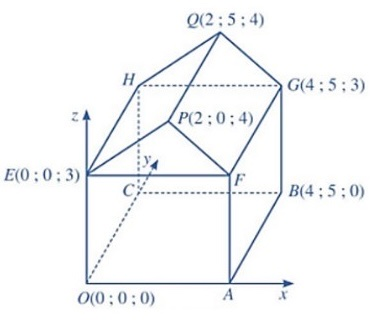
a) Vì nền nhà là hình chữ nhật nên 
là hình chữ nhật, suy ra 
, 
.
Do điểm 
nằm trên trục 
nên tọa độ điểm 
; điểm 
nằm trên trục 
nên tọa độ điểm 
.
Tường nhà là hình chữ nhật nên 
là hình chữ nhật, suy ra 
, 
.
Do 
nằm trên mặt phẳng 
nên tọa độ điểm 
.
Tứ giác 
là hình chữ nhật nên 
, 
Do 
nằm trên mặt phẳng 
nên tọa độ điểm 
.
b) Ta có toạ độ vectơ 
.
c) Ta có 
. Suy ra 
.
d) Để tính góc đốc của mái nhà, ta tính số đo của góc nhị diện có cạnh là đường thẳng 
, hai mặt lần lượt là 
và 
.
Do mặt phẳng 
vuông góc với hai mặt phẳng và nên 
là góc phẳng nhị diện cần tìm.
Ta có 
, 
suy ra
.
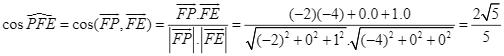Do đó, 
. Vậy góc đốc mái nhà khoảng 
.
Lời giải
a) Đ, b) S, c) Đ, d) S
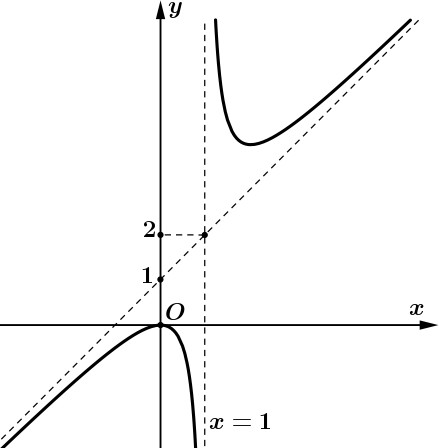
a) Dựa vào đồ thị ta thấy hàm số đồng biến trên khoảng 
.
b) Dựa vào đồ thị ta thấy hàm số đạt cực đại tại 
.
c) Theo đồ thị ta thấy 
và 
.
d) Xét hàm số 
. Vì 
liên tục trên 
nên 
liên tục trên .
Từ đồ thị ta có bảng xét dấu của 
như sau:
Ta có: 
.
Cho 
.
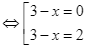
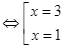Từ bảng xét dấu của suy ra được bảng xét dấu của 
Vậy hàm số không nghịch biến trên 
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận