Cho đường tròn 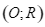 , đường kính
, đường kính 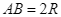 . Vẽ hai tiếp tuyến
. Vẽ hai tiếp tuyến 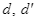 của đường tròn
của đường tròn 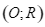 lần lượt tại
lần lượt tại 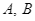 . Trên đường thẳng
. Trên đường thẳng 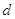 lấy điểm
lấy điểm 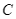 , từ
, từ 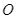 kẻ đường thẳng vuông góc với
kẻ đường thẳng vuông góc với 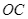 cắt đường thẳng
cắt đường thẳng 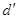 ở
ở 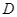 .
Chứng minh
.
Chứng minh 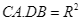 và
và 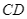 là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn 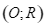 .
.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:

⦁ Ta có ![]()
Suy ra ![]()
Lại có ![]() (tổng hai góc nhọn trong
(tổng hai góc nhọn trong ![]() vuông tại
vuông tại ![]()
Do đó ![]() .
.
Xét ![]() và
và ![]() có:
có: ![]() và
và ![]() .
.
Do đó ![]() (g.g)
(g.g)
Suy ra ![]() nên
nên ![]()
⦁ Vì ![]() suy ra
suy ra ![]()
Mà ![]() nên
nên ![]() .
.
Xét ![]() và
và ![]() có:
có: ![]() và
và ![]()
Do đó ![]() (c.g.c)
(c.g.c)
Suy ra ![]() (hai góc tương ứng).
(hai góc tương ứng).
Kẻ ![]() tại
tại ![]() .
.
Xét ![]() và
và ![]() có:
có:
![]() ,
, ![]() là cạnh chung và
là cạnh chung và ![]()
Do đó ![]() (cạnh huyền – góc nhọn).
(cạnh huyền – góc nhọn).
Suy ra ![]() (hai cạnh tương ứng).
(hai cạnh tương ứng).
Như vậy, ![]() tại
tại ![]() và
và ![]() thuộc đường tròn
thuộc đường tròn ![]() (do
(do ![]() nên
nên ![]() là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) là số lần giảm giá \(10\,\,000\) đồng \(\left( {x \in \mathbb{N},\,\,0 \le x < 20} \right).\)
Giá bán mỗi sản phẩm sau khi giảm giá là: \(200 - 10x\) (nghìn đồng).
Số lượng sản phẩm bán ra sau khi giảm giá là: \(100 + 20x\) (chiếc).
Doanh thu \(T\left( x \right)\) của cửa hàng được tính bằng cách nhân giá bán mỗi sản phẩm với số lượng sản phẩm bán ra:
\(T\left( x \right) = \left( {200 - 10x} \right)\left( {100 + 20x} \right)\)
\( = 200.\left( {100 + 20x} \right) - 10x\left( {100 + 20x} \right)\)
\( = 20\,\,000 + 4\,\,000x - 1\,\,000x - 200{x^2}\)
\( = 20\,\,000 + 3\,\,000x - 200{x^2}\)
\( = - 200\left( {{x^2} - 15x + 7,{5^2}} \right) + 31\,\,250\)
\( = - 200{\left( {x - 7,5} \right)^2} + 31\,\,250\) (nghìn đồng).
Nhận thấy \( - 200{\left( {x - 7,5} \right)^2} + 31\,\,250 \le 31\,\,250\).
Dấu “=” xảy ra khi và chỉ khi \(x - 7,5 = 0\) khi \(x = 7,5\).
Do \(x\) phải là số nguyên dương nên \(x = 7,5\) không thỏa mãn.
Ta thấy rằng \(T\left( x \right) = - 200{\left( {x - 7,5} \right)^2} + 31\,\,250\) lớn nhất khi \({\left( {x - 7,5} \right)^2}\) nhỏ nhất.
Do giá trị của \(T\left( x \right)\) phụ thuộc \(x - 7,5\) và \(x\) nguyên nên ta xét các trường hợp sau:
⦁ Với \(x - 7,5 > 0\) hay \(x > 7,5\).
Mà \(x\) nguyên dương và \({\left( {x - 7,5} \right)^2}\) nhỏ nhất, nên ta lấy giá trị \(x = 8.\)
Khi đó, \(T\left( 8 \right) = 31\,\,200\) (nghìn đồng).
⦁ Với \(x - 7,5 < 0\) hay \(x < 7,5\).
Mà \(x\) nguyên dương và \({\left( {x - 7,5} \right)^2}\) nhỏ nhất, nên ta lấy giá trị \(x = 7.\)
Khi đó, \(T\left( 7 \right) = 31\,\,200\) (nghìn đồng).
Nhận thấy cả hai giá trị \(x = 7,\,\,x = 8\) đều cho doanh thu \(T = 31\,\,200\) (nghìn đồng) hay \(T = 31\,\,200\,\,000\) đồng.
Do đó, cửa hàng nên giảm giá \(70\,\,000\) đồng hoặc \(80\,\,000\) đồng để thu được doanh thu cao nhất.
Lời giải

Vì ![]() là hai tiếp tuyến của đường tròn
là hai tiếp tuyến của đường tròn ![]() lần lượt tại
lần lượt tại ![]() nên
nên ![]() .
.
Tứ giác ![]() có
có ![]() (cùng vuông góc với
(cùng vuông góc với ![]() ) nên
) nên ![]() là hình thang.
là hình thang.
Hình thang ![]() có
có ![]() nên
nên ![]() là hình thang vuông.
là hình thang vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.