Cho hai biểu thức: \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\) và \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\).
a) Tìm điều kiện xác định của biểu thức \(A\) và \(B.\)
b) Tính giá trị của biểu thức \(A\) khi \(x = \frac{1}{9}.\)
c) Rút gọn biểu thức \(B.\)
d) Tìm giá trị nhỏ nhất của biểu thức \(P = A.B\) với \(x > 1.\)
Cho hai biểu thức: \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\) và \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\).
a) Tìm điều kiện xác định của biểu thức \(A\) và \(B.\)
b) Tính giá trị của biểu thức \(A\) khi \(x = \frac{1}{9}.\)
c) Rút gọn biểu thức \(B.\)
d) Tìm giá trị nhỏ nhất của biểu thức \(P = A.B\) với \(x > 1.\)
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
a) – Xét biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\).
Điều kiện xác định của biểu thức \(A\) và \(x \ge 0\) và \(\sqrt x - 1 \ne 0\) hay \(x \ge 0,\,\,x \ne 1.\)
– Xét biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\).
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(x + \sqrt x \ne 0,\,\,x - 1 \ne 0,\,\,x - \sqrt x \ne 0.\)
Với mọi \(x \ge 0,\) ta có:
⦁ \(x - 1 = \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)\).
Lại có \(\sqrt x \ge 0\) nên \(\sqrt x + 1 \ge 1 > 0.\)
Do đó \(x - 1 \ne 0\) khi \(\sqrt x - 1 \ne 0,\) hay \(\sqrt x \ne 1,\) tức là \(x \ne 1.\)
⦁ \(x + \sqrt x = \sqrt x \left( {\sqrt x + 1} \right)\)
Lại có \(\sqrt x \ge 0\) nên \(\sqrt x + 1 \ge 1 > 0.\)
Do đó \(x + \sqrt x \ne 0\) khi \(\sqrt x \ne 0\) hay \(x \ne 0\).
⦁ \(x - \sqrt x = \sqrt x \left( {\sqrt x - 1} \right)\)
Do đó \(x - \sqrt x \ne 0\) khi \(\sqrt x \ne 0\) và \(\sqrt x - 1 \ne 0\), tức là \(x \ne 0\) và \(x \ne 1.\)
Như vậy, điều kiện xác định của biểu thức \(B\) là \(x > 0,x \ne 1.\)
Vậy, điều kiện xác định của biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\) là \(x \ge 0,x \ne 1\) và điều kiện xác định của biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\) là \(x > 0,x \ne 1.\)
b) Thay \(x = \frac{1}{9}\) (thỏa mãn điều kiện) vào biểu thức \(A,\) ta được:
\(A = \frac{{\sqrt {\frac{1}{9}} \left( {\frac{1}{9} + 1} \right)}}{{2\left( {\sqrt {\frac{1}{9}} - 1} \right)}} = \frac{{\frac{1}{3}.\frac{{10}}{9}}}{{2\left( {\frac{1}{3} - 1} \right)}} = \frac{{\frac{{10}}{{27}}}}{{ - \frac{4}{3}}} = - \frac{5}{{18}}.\)
Vậy \(A = - \frac{5}{{18}}\) khi \(x = \frac{1}{9}\).
c) Với \(x > 0,x \ne 1\), ta có:
\(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\)
\( = \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}} + \frac{{2\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}\)
\[ = \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2\sqrt x \cdot \sqrt x }}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{\sqrt x + 1}}{{\sqrt x \left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\( = \frac{{\sqrt x - 1 + 2x - \sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)\( = \frac{{2x - 2}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{2\left( {x - 1} \right)}}{{\sqrt x \left( {x - 1} \right)}}\)\( = \frac{2}{{\sqrt x }}\).
Vậy với \(x > 0,x \ne 1\) thì \(B = \frac{2}{{\sqrt x }}\).
d) Với \(x > 1,\) ta có:
\(P = A.B = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}.\frac{2}{{\sqrt x }} = \frac{{x + 1}}{{\sqrt x - 1}} = \frac{{x - 1 + 2}}{{\sqrt x - 1}} = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}{{\sqrt x - 1}} + \frac{2}{{\sqrt x - 1}} = \sqrt x + 1 + \frac{2}{{\sqrt x - 1}}\).
Xét \(P = \sqrt x + 1 + \frac{2}{{\sqrt x - 1}} = \sqrt x - 1 + \frac{2}{{\sqrt x - 1}} + 2\) với \(x > 1.\)
Do \(x > 1\) nên \(\sqrt x - 1 > 0\).
Áp dụng bất đẳng thức Cauchy cho 3 số \(\sqrt x - 1\,;\,\,\frac{2}{{\sqrt x - 1}}\,;\,\,2\) không âm, ta có:
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} \ge 2\sqrt {\left( {\sqrt x - 1} \right).\frac{2}{{\sqrt x - 1}}} \)
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} \ge 2\sqrt 2 \)
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} + 2 \ge 2\sqrt 2 + 2\)
Suy ra \(P \ge 2\sqrt 2 + 2\) với \(x > 1\).
Dấu “=” xảy ra khi và chỉ khi \(\sqrt x - 1 = \frac{2}{{\sqrt x - 1}}\) .
Giải phương trình:
\(\sqrt x - 1 = \frac{2}{{\sqrt x - 1}}\)
\({\left( {\sqrt x - 1} \right)^2} = 2\)
\(\sqrt x - 1 = \sqrt 2 \) (do \(\sqrt x - 1 > 0)\)
\(\sqrt x = \sqrt 2 + 1\)
\(x = 3 + 2\sqrt 2 \) (thỏa mãn).
Vậy giá trị nhỏ nhất của \(P = 2\sqrt 2 + 2\) khi \(x = 3 + 2\sqrt 2 \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
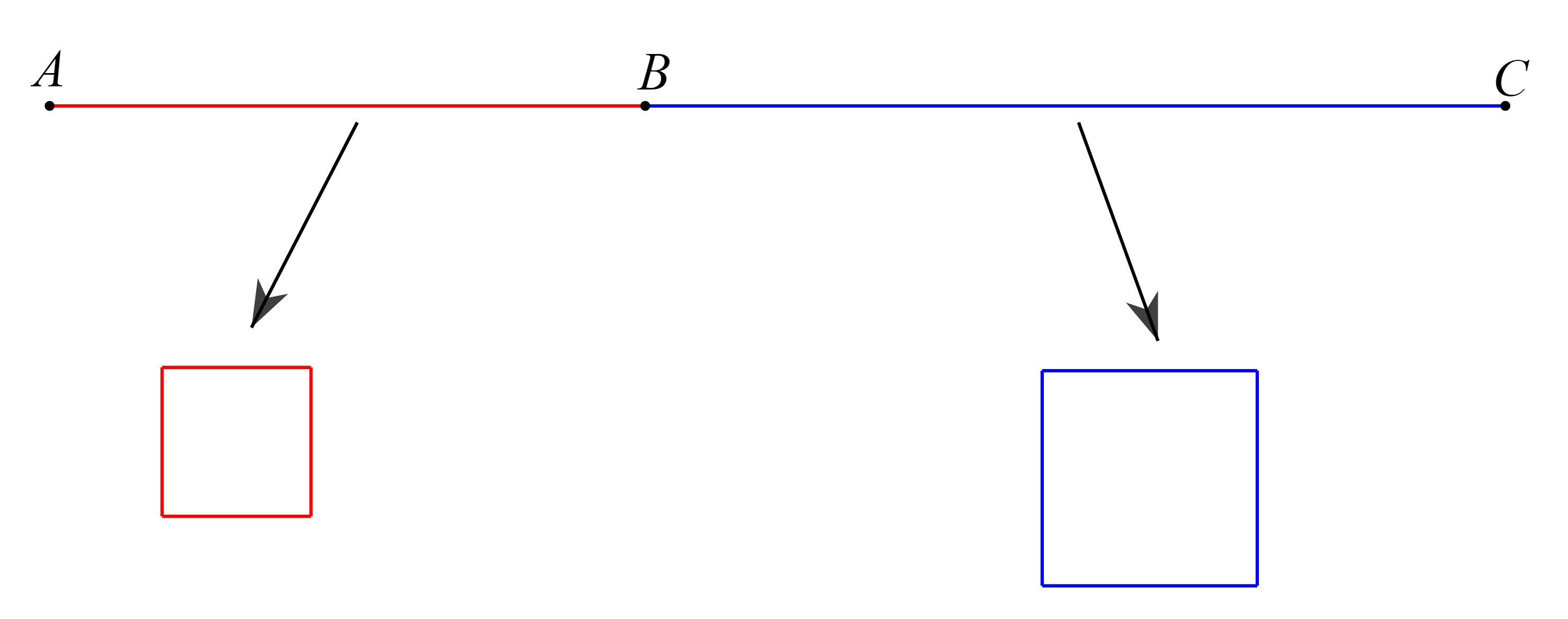
Gọi cạnh hình vuông được uốn từ đoạn ![]() là
là ![]() (
(![]()
, đơn vị: m).
Lúc này, độ dài đoạn ![]() chính là chu vi hình vuông đó và bằng
chính là chu vi hình vuông đó và bằng ![]() (m).
(m).
Do đó, độ dài đoạn ![]() là
là ![]() (m).
(m).
Suy ra, độ dài cạnh hình vuông được uốn bởi đoạn ![]() là
là ![]() (m).
(m).
Tổng diện tích hai hình vuông lúc này là: ![]()
Ta có: ![]() .
.
Tổng diện tích hai hình vuông đạt giá trị nhỏ nhất bằng ![]() khi
khi ![]() hay
hay ![]()
Khi đó, độ dài đoạn thẳng ![]() và độ dài đoạn thẳng
và độ dài đoạn thẳng ![]() hay
hay ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() .
.
Vậy để tổng diện tích hai hình vuông đạt giá trị nhỏ nhất thì ta chia đoạn dây thép thành hai phần bằng nhau ![]()
Lời giải
Gọi ![]() là số sản phẩm đội phải làm theo kế hoạch (
là số sản phẩm đội phải làm theo kế hoạch (![]() , đơn vị: sản phẩm) và
, đơn vị: sản phẩm) và ![]() là số ngày đội đó làm theo kế hoạch (
là số ngày đội đó làm theo kế hoạch (![]() , đơn vị: ngày).
, đơn vị: ngày).
Theo kế hoạch, số sản phẩm phải làm là: ![]() (1).
(1).
Thực tế, mỗi ngày đội làm được 60 sản phẩm và hoàn thành trước 2 ngày đồng thời làm thêm được 24 sản phẩm.
Do đó, dựa vào số sản phẩm thực tế, ta có phương trình: ![]() hay
hay ![]() (2).
(2).
Từ (1) và (2) ta có hệ phương trình: 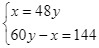 .
.
Thay ![]() vào phương trình (2), ta được:
vào phương trình (2), ta được:
![]() , suy ra
, suy ra ![]() nên
nên ![]() (thỏa mãn).
(thỏa mãn).
Thay ![]() vào phương trình
vào phương trình ![]() , được
, được ![]() (thỏa mãn).
(thỏa mãn).
Vậy số sản phẩm đội đó phải làm theo kế hoạch là ![]() sản phẩm.
sản phẩm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.