Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
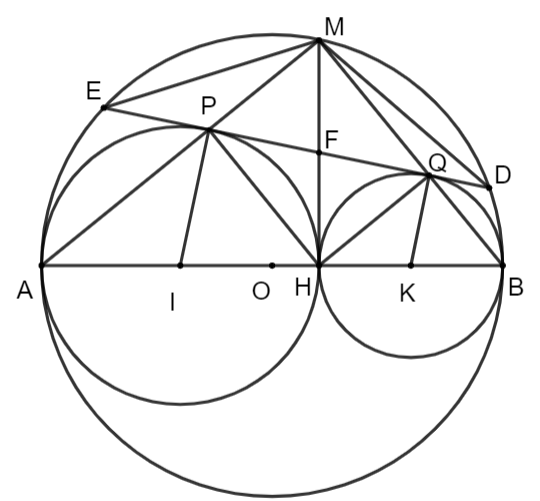
⦁ Chứng minh tam giác ![]() là tam giác cân
là tam giác cân
Theo câu b, ![]() suy ra
suy ra ![]() .
.
Xét ![]() và
và ![]() có:
có: ![]() là góc chung và
là góc chung và ![]()
Do đó ![]() (c.g.c), suy ra
(c.g.c), suy ra ![]() (hai góc tương ứng).
(hai góc tương ứng).
Ta có: ![]() nên tam giác
nên tam giác ![]() cân ở
cân ở ![]() , suy ra
, suy ra ![]() .
.
Mà ![]() suy ra
suy ra ![]() nên
nên ![]() .
.
Xét ![]() cân ở
cân ở ![]() (do
(do ![]() ) có
) có ![]() là đường cao nên
là đường cao nên ![]() cũng là đường trung trực của
cũng là đường trung trực của ![]() . Suy ra
. Suy ra ![]() nên
nên ![]() cân ở
cân ở ![]() .
.
⦁ Xác định vị trí của ![]() để chu vi tứ giác
để chu vi tứ giác ![]() lớn nhất
lớn nhất
Chứng minh tương tự câu c, ta có ![]() là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn ![]() tại
tại ![]()
Ta có: ![]() suy ra
suy ra ![]() , do đó tứ giác
, do đó tứ giác ![]() là hình thang.
là hình thang.
Lại có ![]() nên hình thang
nên hình thang ![]() là hình thang vuông.
là hình thang vuông.
Ta có chu vi ![]() là
là ![]()
![]()
![]() (do
(do ![]()
![]()
![]() .
.
Lại có ![]() và
và ![]()
Do đó ![]() , suy ra
, suy ra ![]()
Hay ![]() .
.
Dấu “=” xảy ra khi và chỉ khi ![]() . Mà
. Mà ![]() (chứng minh ở câu c) nên
(chứng minh ở câu c) nên ![]()
Lại có ![]() là đường kính của đường tròn
là đường kính của đường tròn ![]() và điểm
và điểm ![]() nằm trên đường tròn
nằm trên đường tròn ![]() nên lúc này điểm
nên lúc này điểm ![]() trùng điểm
trùng điểm ![]() tức là
tức là ![]() tại tâm
tại tâm ![]() . Như vậy, điều này xảy ra khi và chỉ khi
. Như vậy, điều này xảy ra khi và chỉ khi ![]() nằm chính giữa cung
nằm chính giữa cung ![]() .
.
Vậy chu vi ![]() đạt giá trị lớn nhất là
đạt giá trị lớn nhất là ![]() khi
khi ![]() nằm chính giữa cung
nằm chính giữa cung ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
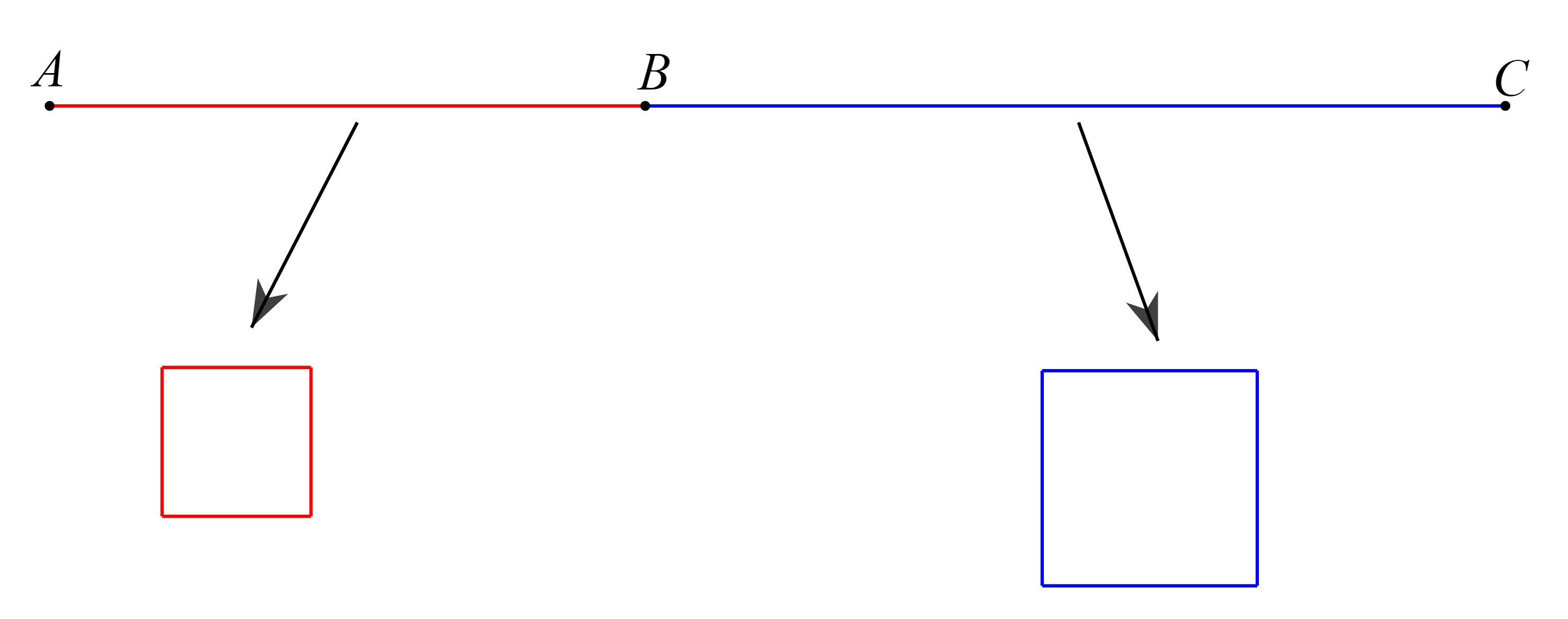
Gọi cạnh hình vuông được uốn từ đoạn ![]() là
là ![]() (
(![]()
, đơn vị: m).
Lúc này, độ dài đoạn ![]() chính là chu vi hình vuông đó và bằng
chính là chu vi hình vuông đó và bằng ![]() (m).
(m).
Do đó, độ dài đoạn ![]() là
là ![]() (m).
(m).
Suy ra, độ dài cạnh hình vuông được uốn bởi đoạn ![]() là
là ![]() (m).
(m).
Tổng diện tích hai hình vuông lúc này là: ![]()
Ta có: ![]() .
.
Tổng diện tích hai hình vuông đạt giá trị nhỏ nhất bằng ![]() khi
khi ![]() hay
hay ![]()
Khi đó, độ dài đoạn thẳng ![]() và độ dài đoạn thẳng
và độ dài đoạn thẳng ![]() hay
hay ![]() là trung điểm của đoạn
là trung điểm của đoạn ![]() .
.
Vậy để tổng diện tích hai hình vuông đạt giá trị nhỏ nhất thì ta chia đoạn dây thép thành hai phần bằng nhau ![]()
Lời giải
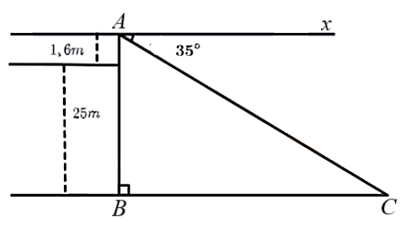
Gọi ![]() là số sản phẩm đội phải làm theo kế hoạch (
là số sản phẩm đội phải làm theo kế hoạch (![]() , đơn vị: sản phẩm) và
, đơn vị: sản phẩm) và ![]() là số ngày đội đó làm theo kế hoạch (
là số ngày đội đó làm theo kế hoạch (![]() , đơn vị: ngày).
, đơn vị: ngày).
Theo kế hoạch, số sản phẩm phải làm là: ![]() (1).
(1).
Thực tế, mỗi ngày đội làm được 60 sản phẩm và hoàn thành trước 2 ngày đồng thời làm thêm được 24 sản phẩm.
Do đó, dựa vào số sản phẩm thực tế, ta có phương trình: ![]() hay
hay ![]() (2).
(2).
Từ (1) và (2) ta có hệ phương trình: 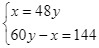 .
.
Thay ![]() vào phương trình (2), ta được:
vào phương trình (2), ta được:
![]() , suy ra
, suy ra ![]() nên
nên ![]() (thỏa mãn).
(thỏa mãn).
Thay ![]() vào phương trình
vào phương trình ![]() , được
, được ![]() (thỏa mãn).
(thỏa mãn).
Vậy số sản phẩm đội đó phải làm theo kế hoạch là ![]() sản phẩm.
sản phẩm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.