Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 2025\), (tham số \(m\)). Xét tính đúng sai của các khẳng định sau
a) Khi \(m = 1\) thì hàm số đạt cực tiểu tại \(x = 2\).
b) Khi \(m = 1\) thì hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
c) Khi \(m = 1\) thì hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\) bằng \( - 4\).
d) Có tất cả 1 giá trị nguyên của \(m\) để hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\).
Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 2025\), (tham số \(m\)). Xét tính đúng sai của các khẳng định sau
a) Khi \(m = 1\) thì hàm số đạt cực tiểu tại \(x = 2\).
b) Khi \(m = 1\) thì hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
c) Khi \(m = 1\) thì hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\) bằng \( - 4\).
d) Có tất cả 1 giá trị nguyên của \(m\) để hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Đ, b) S, c) S, d) S
Ta có \(y' = 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right)\).
Với \(m = 1\), ta có \(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
Ta có bảng biến thiên
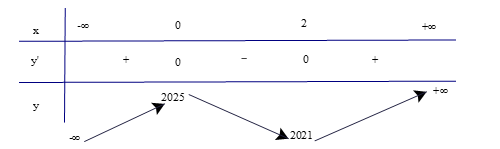
Dựa vào bảng biến thiên,
a) Hàm số đạt cực tiểu tại \(x = 2\).
b) Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
c) Hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\) bằng \(2021\).
d) Ta có \(y' = 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = m - 1\\{x_2} = m + 1\end{array} \right.\).
Để hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\) thì \({x_1} \le 0 < {x_2}\) hoặc \(0 < {x_1} < {x_2}\).
TH1: \({x_1} \le 0 < {x_2}\)\( \Leftrightarrow m - 1 \le 0 < m + 1 \Leftrightarrow - 1 < m \le 1\). Do \(m \in \mathbb{Z}\) nên \(m \in \left\{ {0;1} \right\}\).
Bảng biến thiên
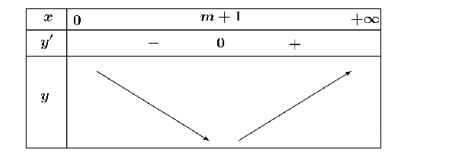
TH2: \(0 < {x_1} < {x_2}\)
Bảng biến thiên của hàm số
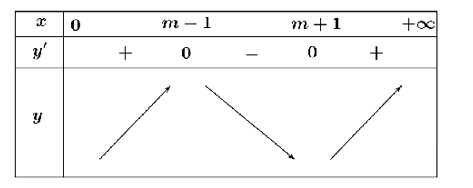
Hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\)khi và chỉ khi \(\left\{ \begin{array}{l}m - 1 > 0\\y\left( {m + 1} \right) \le y\left( 0 \right)\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 1\\{\left( {m + 1} \right)^3} - 3m{\left( {m + 1} \right)^2} + 3\left( {{m^2} - 1} \right)\left( {m + 1} \right) + 2025 \le 2025\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > 1\\{\left( {m + 1} \right)^2}\left( {m - 2} \right) \le 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 1\\\left[ \begin{array}{l}m \le 2\\m = - 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow 1 < m \le 2\). Do \(m \in \mathbb{Z}\) nên \(m = 2\).
Vậy có tất cả 3 giá trị của \(m\).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất với trục \(Ox\) hướng về phía nam, trục \(Oy\) hướng về phía đông và trục \({\rm{Oz}}\) hướng thẳng đứng lên trời (tham khảo hình vẽ), đơn vị đo lấy theo kilômét.
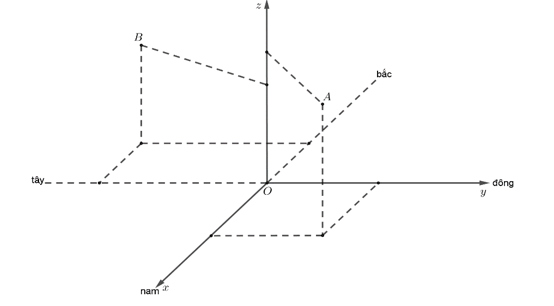
Chiếc khinh khí cầu thứ nhất và thứ hai ở vị trí \(A,B\). Ta có \(A\left( {\frac{5}{2};2;\frac{4}{5}} \right),B\left( { - \frac{3}{2}; - 3;\frac{3}{5}} \right)\).
Gọi \(C\) là điểm đối xứng của \(A\) qua mặt phẳng \(\left( {Oxy} \right)\), \(C\left( {\frac{5}{2};2; - \frac{4}{5}} \right)\).
Khi đó \(I = BC \cap \left( {Oxy} \right)\).
\(\overrightarrow {BC} = \left( {4;5; - \frac{7}{5}} \right)\). \(I \in \left( {Oxy} \right) \Rightarrow I\left( {x;y;0} \right) \Rightarrow \overrightarrow {BI} = \left( {x + \frac{3}{2};y + 3; - \frac{3}{5}} \right)\)
\(\overrightarrow {BC} ,\overrightarrow {BI} \) cùng phương nên \(\frac{{x + \frac{3}{2}}}{4} = \frac{{y + 3}}{5} = \frac{3}{7} \Rightarrow \left\{ \begin{array}{l}x = \frac{3}{{14}}\\y = - \frac{6}{7}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{3}{{14}}\\b = \frac{6}{7}\end{array} \right. \Rightarrow 2a + 3b = 3\).
Lời giải
Ta có \(C'\left( v \right) = - \frac{{5400}}{{{v^2}}} + \frac{3}{2} = \frac{{3\left( {v - 60} \right)\left( {v + 60} \right)}}{{2{v^2}}}\);
\(C'\left( v \right) = 0\)\( \Leftrightarrow v = - 60\)(loại) hoặc \(v = 60\) (nhận).
Trên khoảng \(\left( {0;60} \right)\), \(C'\left( v \right) < 0\) nên hàm số nghịch biến trên khoảng này.
Trên khoảng \(\left( {60;120} \right)\), \(C'\left( v \right) > 0\) nên hàm số đồng biến trên khoảng này.
Hàm số đạt cực tiểu tại \(v = 60,{C_{CT}} = C\left( {60} \right) = 180\).
Như vậy để tiết kiệm xăng nhất tài xế nên chạy xe với tốc độ trung bình là 60 km/h.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập