Ý nghĩa độ lệch chuẩn của mẫu số liệu ghép nhóm
A. dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó.
B. cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu.
C. chia mẫu số liệu thành hai phần, mỗi phần chứa 50% giá trị.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Ý nghĩa độ lệch chuẩn của mẫu số liệu ghép nhóm: Độ lệch chuẩn của mẫu số liệu ghép nhóm xấp xỉ cho độ lệch chuẩn của mẫu số liệu gốc. Độ lệch chuẩn được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
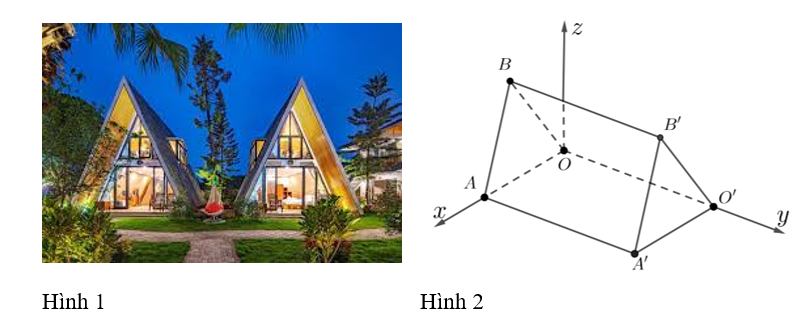
Vì điểm \(A'\) có toạ độ là \(\left( {240;450;0} \right)\) nên khoảng cách từ \(A'\) đến các trục \(Ox,Oy\) lần lượt là \(450\;{\rm{cm}}\) và \(240\;{\rm{cm}}\). Suy ra \(A'A = 450\;{\rm{cm}}\) và \(A'O' = 240\;{\rm{cm}}\).
Từ giả thiết suy ra \(\overrightarrow {A'B'} = \left( { - 120;0;300} \right)\),
do đó \(A'B' = \left| {\overrightarrow {A'B'} } \right| = \sqrt {{{( - 120)}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323(\;{\rm{cm}})\).
Vì \(O'O = A'A = 450\;{\rm{cm}}\) và \(O'\) nằm trên trục \[Oy\] nên toạ độ của điểm \(O'\) là \(\left( {0;450;0} \right)\).
Do đó \(\overline {O'B'} = \left( {120;0;300} \right)\) và \(O'B' = \left| {\overline {O'B'} } \right| = \sqrt {{{120}^2} + {0^2} + {{300}^2}} = 60\sqrt {29} \approx 323{\rm{ }}({\rm{cm}})\).
Vậy mỗi căn lều gỗ có chiều dài là \(450\;{\rm{cm}}\), chiều rộng là \(240\;{\rm{cm}}\), mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
\( \Rightarrow a + b + c = 1013\).
Lời giải
Ta có \(N'\left( t \right) = - 3{t^2} + 24t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 8\end{array} \right.\).
Bảng biến thiên
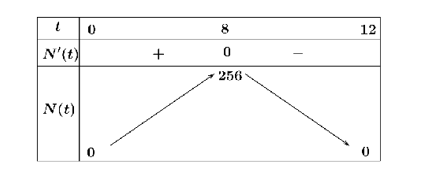
Từ bảng biến thiên ta thấy số người bị nhiễm bệnh tăng trong khoảng thời gian \(\left( {0;8} \right)\).
Suy ra \(a = 0;b = 8\). Vậy \(a + b = 8\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.