Ánh sáng màu vàng có bước sóng 589 nm được dùng trong thí nghiệm hai khe Young. Khoảng cách hai khe là 0,20 mm và màn đặt cách hai khe 1,20 m.
a) Tính khoảng vân của hệ vân giao thoa tạo thành trên màn.
b) Trên vùng quan sát vân giao thoa rộng \[L = 46,0{\rm{ }}mm\] sẽ quan sát được bao nhiêu vân sáng, vân tối?
Ánh sáng màu vàng có bước sóng 589 nm được dùng trong thí nghiệm hai khe Young. Khoảng cách hai khe là 0,20 mm và màn đặt cách hai khe 1,20 m.
a) Tính khoảng vân của hệ vân giao thoa tạo thành trên màn.
b) Trên vùng quan sát vân giao thoa rộng \[L = 46,0{\rm{ }}mm\] sẽ quan sát được bao nhiêu vân sáng, vân tối?
Câu hỏi trong đề: 17 bài tập Chủ đề 2. Sóng có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Khoảng vân: \[i = \frac{{\lambda D}}{a} = \frac{{{{589.10}^{ - 9}}.1,2}}{{0,{{2.10}^{ - 3}}}} = 3,{5.10^{ - 3}}\,m\].
b) Số vân sáng quan sát được trên màn: \[{N_s} = 2\left[ {\frac{L}{{2i}}} \right] + 1 = 2\left[ {\frac{{46}}{{2.3,5}}} \right] + 1 = 13\]vân.
Số vân tối trên màn: \[{N_t} = 2\left[ {\frac{L}{{2i}} + 0,5} \right] = 2\left[ {\frac{{46}}{{2.3,5}} + 0,5} \right] = 14\] vân.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Ta có: \(I = \frac{{25,0}}{{4\pi {{\left( {2,02 \cdot {{10}^7}} \right)}^2}}} \approx 4,88 \cdot {10^{ - 15}}{\rm{\;W/}}{{\rm{m}}^{\rm{2}}}\).
b) Bước sóng của tín hiệu mà trạm thu sóng nhận được là: \(\lambda = \frac{{3,{{0.10}^8}}}{{1575,42 \cdot {{10}^6}}} \approx 0,19{\rm{\;m}}.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
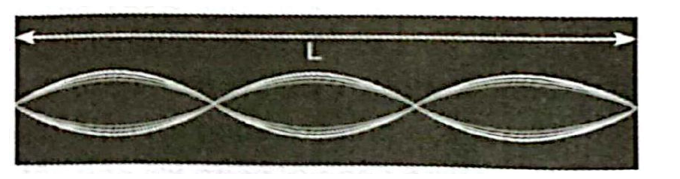
a) Trên hình vẽ các định được k = 3:
\(L = 3\frac{\lambda }{2} \Rightarrow \lambda = \frac{{2.{\rm{L}}}}{3} = \frac{{2 \cdot 0,9}}{3} = 0,6{\rm{\;m}}\).
b) \(v = \lambda f = 0,6.180 = 108{\rm{\;m}}/{\rm{s}}\).
c) \(\left. {\begin{array}{*{20}{l}}{{v_1} = {f_1}{\lambda _1}}\\{{v_2} = {f_2}{\lambda _2}}\end{array}} \right\} \Rightarrow \frac{{{f_1}{\lambda _1}}}{{{f_2}{\lambda _2}}} = 1 \Rightarrow {\lambda _2} = \frac{{{f_1}{\lambda _1}}}{{{f_2}}} = \frac{{180 \cdot 0,6}}{{360}} = 0,3{\rm{\;m}}\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập