khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Vào học
Đăng nhập
Tạo VIP
Xin chào! Vào học
  2. Tốt nghiệp THPT
  3. Vật lý

Câu hỏi:

19/08/2025 1,712 Lưu

Hình dưới mô tả sóng dừng trên một sợi dây có chiều dài L = 0,9 m, hai đầu cố định.

Hình dưới mô tả sóng dừng trên một sợi dây có chiều dài L = 0,9 m, hai đầu cố định. (ảnh 1)

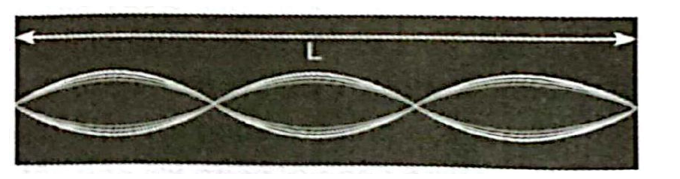
a) Tính bước sóng \(\lambda \) của sóng trên dây.

b) Nếu tần số là 180 Hz. Tính tốc độ của sóng.

c) Thay đổi tần số đến 360 Hz thì bước sóng bây giờ bằng bao nhiêu?

Xem lời giải

Câu hỏi trong đề: 17 bài tập Chủ đề 2. Sóng có lời giải !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

a) Trên hình vẽ các định được k = 3:

\(L = 3\frac{\lambda }{2} \Rightarrow \lambda = \frac{{2.{\rm{L}}}}{3} = \frac{{2 \cdot 0,9}}{3} = 0,6{\rm{\;m}}\).

b) \(v = \lambda f = 0,6.180 = 108{\rm{\;m}}/{\rm{s}}\).

c) \(\left. {\begin{array}{*{20}{l}}{{v_1} = {f_1}{\lambda _1}}\\{{v_2} = {f_2}{\lambda _2}}\end{array}} \right\} \Rightarrow \frac{{{f_1}{\lambda _1}}}{{{f_2}{\lambda _2}}} = 1 \Rightarrow {\lambda _2} = \frac{{{f_1}{\lambda _1}}}{{{f_2}}} = \frac{{180 \cdot 0,6}}{{360}} = 0,3{\rm{\;m}}\).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hệ thống định vị toàn cầu (GPS - Global Positioning System) gồm 24 vệ tinh nhân tạo. Mỗi vệ tinh thực hiện hai vòng quay quanh Trái Đất trong một ngày ở độ cao 2,02.107 m đối với mặt đất và phát tín hiệu điện từ đẳng hướng có công suất 25 W về phía mặt đất. Một trong các tín hiệu điện từ này có tần số 1 575,42 MHz.

a) Tính cường độ tín hiệu điện từ nhận được ở trạm thu sóng tại một vị trí trên mặt đất ngay ở phía dưới một vệ tinh.

b) Trạm thu sóng nhận được tín hiệu có bước sóng bằng bao nhiêu?

Lời giải

a) Ta có: \(I = \frac{{25,0}}{{4\pi {{\left( {2,02 \cdot {{10}^7}} \right)}^2}}} \approx 4,88 \cdot {10^{ - 15}}{\rm{\;W/}}{{\rm{m}}^{\rm{2}}}\).

b) Bước sóng của tín hiệu mà trạm thu sóng nhận được là: \(\lambda = \frac{{3,{{0.10}^8}}}{{1575,42 \cdot {{10}^6}}} \approx 0,19{\rm{\;m}}.\)

Câu 2

Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn A, B dao động cùng pha với cùng tần số \[f = 13{\rm{ }}Hz\]. Tại một điểm M cách các nguồn A, B lần lượt là \[{d_1} = 19\,\,cm\], \[{d_2} = 21\,\,cm\]thì sóng có biên độ cực đại. Giữa M và đường trung trực của AB không có dãy cực đại khác. Tốc độ truyền sóng trên mặt nước là
A. v = 26 m/s.         
B. v = 52 m/s.         
C. v = 26 cm/s.        
D. v = 52 cm/s.

Lời giải

M là điểm cực đại nên: \[{d_2} - {d_1} = k\lambda = k.\frac{v}{f} \Rightarrow 21 - 19 = k.\frac{v}{{13}}\]

Do giữa M và đường trung trực của AB không có dãy cực đại khác nên M thuộc dãy cực đại bậc 1, nên k = 1.

\[ \Rightarrow 21 - 19 = \frac{v}{{13}} \Rightarrow v = 26\,cm/s\]. Chọn C.

Câu 3

Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn sóng A và B dao động với phương trình \({u_{\rm{A}}} = {u_{\rm{B}}} = 5{\rm{cos}}10\pi t\left( {{\rm{cm}}} \right)\). Biết tốc độ truyền sóng là 20 cm/s.

a) Viết phương trình dao động của điểm M trên mặt nước cách A, B lần lượt 7,2 cm và 8,2 cm.

b) Một điểm N trên mặt nước có \({\rm{AN}} - {\rm{BN}} = 10{\rm{\;cm}}\). Điểm N nằm trên dãy gồm những điểm dao động với biên độ cực đại hay đứng yên?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong thí nghiệm Young về giao thoa ánh sáng, hai khe cách nhau \[a = 0,5{\rm{ }}mm\] và được chiếu sáng bằng ánh sáng đơn sắc có bước sóng λ. Khoảng cách từ hai khe đến màn quan sát là 2 m. Trên màn quan sát, trong vùng giữa hai điểm M và N mà MN = 2 cm, người ta thấy tại M và N đều là vân sáng và đếm được có 10 vân tối. Bước sóng \[\lambda \] của ánh sáng dùng trong thí nghiệm này là
A. 0,4 μm.               
B. 0,5 μm.              
C. 0,6 μm.                 
D. 0,7 μm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Xét một sóng dừng trên dây có hai đầu cố định được hình thành từ dao động của sóng âm ở hoạ âm bậc ba. Tốc độ truyền sóng trên dây là 192 m/s và tần số sóng là 240 Hz. Biên độ dao động tại bụng sóng là 0,40 cm. Tính biên độ dao động của điểm M và N trên dây. Biết khoảng cách từ điểm M, N đến một đầu dây lần lượt là 40,0 cm và 20,0 cm.

 

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Ánh sáng màu vàng có bước sóng 589 nm được dùng trong thí nghiệm hai khe Young. Khoảng cách hai khe là 0,20 mm và màn đặt cách hai khe 1,20 m.

a) Tính khoảng vân của hệ vân giao thoa tạo thành trên màn.

b) Trên vùng quan sát vân giao thoa rộng \[L = 46,0{\rm{ }}mm\] sẽ quan sát được bao nhiêu vân sáng, vân tối?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập