Cho tam giác ABC vuông tại A, cạnh AB = 4 cm, \(\widehat B\) = 50°. Đường tròn tâm I, đường kính AB cắt BC ở D. Chọn khẳng định sai?
A. \(\widehat {BCA} = 40^\circ \).
B. Độ dài cung nhỏ BD của (I) là \(\frac{{8\pi }}{9}\) cm.
C. \(\widehat {DAC} = 50^\circ \).
D. Độ dài cung lớn BD của (I) là \(\frac{{3\pi }}{2}\) cm.
Câu hỏi trong đề: 12 bài tập Tính độ dài đường tròn, cung tròn có lời giải !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
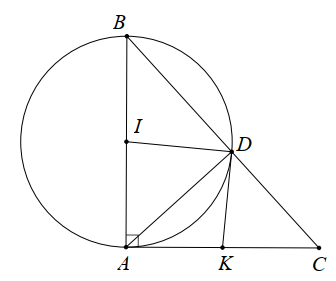
Xét tam giác ABC vuông tại A có \(\widehat B\) = 50° nên \(\widehat C\) = 90° − 50° = 40°. Do đó A đúng.
Xét đường tròn (I) đường kính AB có \(\widehat {BDA} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn), suy ra \(\widehat {DAC} = \widehat B = 50^\circ \) (cùng phụ với góc \(\widehat {DAB}\)) nên C đúng.
Vì \(\widehat {DAC} = \widehat B = 50^\circ \) nên \(\widehat {DAB} = 90^\circ - 50^\circ - 40^\circ \) suy ra số đo cung BD nhỏ là:
n° = 2.40° = 80°.
Độ dài cung nhỏ BD của (I) là l = \(\frac{{\pi .\frac{4}{2}.80}}{{180}} = \frac{{8\pi }}{9}{\rm{ }}(cm)\) nên B đúng.
Số đo cung lớn BD là 360° − 80° = 280°.
Độ dài cung lớn BD là: l1 = \(\frac{{\pi .\frac{4}{2}.280}}{{180}} = 3\pi {\rm{ }}(cm)\) nên D sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Độ dài cung nhỏ BD của (I) là \(\frac{\pi }{6}\) (cm).
B. AD ⊥ BC.
C. D thuộc đường tròn đường kính AC.
D. Độ dài cung nhỏ BD của (I) là \(\frac{{5\pi }}{6}\) cm.
Lời giải
Đáp án đúng là: A
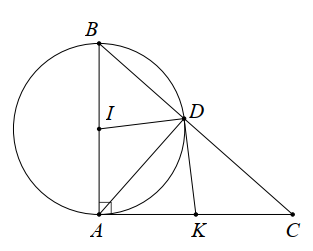
Xét đường tròn (I) đường kính AB có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Nên AD ⊥ BC. Do đó đáp án B đúng.
Gọi K là trung điểm của AC, suy ra KA = KC = KD. Do đó K thuộc đường tròn đường kính AC. Do đó đáp án C đúng.
Ta có ∆IBD cân tại I có \(\widehat B = 60^\circ \), suy ra ∆IBD đều nên \(\widehat {DIB} = 60^\circ \).
Độ dài cung nhỏ BD của (I) là:
l = \(\frac{{\pi .\frac{5}{2}.60}}{{180^\circ }} = \frac{{5\pi }}{6}\) (cm).
Do đó đáp án D đúng.
Câu 2
A. \(\frac{{2\pi R}}{3}\).
B. \(\frac{{5\pi R}}{3}\).
C. \(\frac{{7\pi R}}{3}\)
D. \(\frac{{4\pi R}}{3}\).
Lời giải
Đáp án đúng là: A
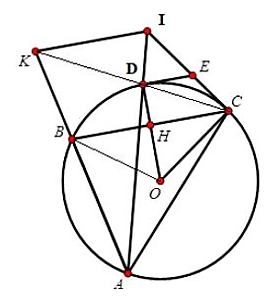
Gọi H là giao điểm của OD và BC thì H là trung điểm của BC (do OD ⊥ BC tại H).
Suy ra HC = \(\frac{{BC}}{2} = \frac{{R\sqrt 3 }}{2}\).
Xét tam giác vuông HOC có sinHOC = \(\frac{{HC}}{{OC}} = \frac{{\sqrt 3 }}{2}\) suy ra \(\widehat {HOC} = 60^\circ \), suy ra
\(\widehat {BOC} = 120^\circ \).
Độ dài cung nhỏ BC là l = \( = \frac{{\pi R.120}}{{180}} = \frac{{2\pi R}}{3}\) (cm)
Câu 3
A. 6,22π.
B. 3,11π.
C. 6π.
D. 12,44π.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{{4\pi }}{3}\).
B. 8π.
C. 4π.
D. 2π.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{{4\pi }}{3}\).
B. \(\frac{{5\pi }}{3}\).
C. \(\frac{{7\pi }}{3}\).
D. \(\frac{{8\pi }}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.