Giải các phương trình sau:

a) \(\frac{2}{3}x + 2\frac{1}{2} = 0\).  b) \(x - 4x + 2x - 29 = 4x + 1\).

c) \(\frac{{2x - 1}}{3} - \frac{{x + 7}}{4} = \frac{{5 - 3x}}{2}\).  d) \[2x\left( {x--1} \right) = {x^2} - 1.\]

a) Xét \(\Delta ABC\) vuông tại \(A,\) theo định lí Pytagore ta có: \(B{C^2} = A{B^2} + A{C^2} = {8^2} + {6^2} = 64 + 36 = 100\) Suy ra \(BC = \sqrt {100} = 10{\rm{\;cm}}.\) Vì \(BD\) là tia phân giác của góc \(ABC\) nên suy ra: \[\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}.\] b) Theo đề bài, \(CE \bot BD\) tại \(E\) nên \(\widehat {BEC} = 90^\circ .\) Xét \(\Delta ABD\) và \(\Delta EBC\) có:

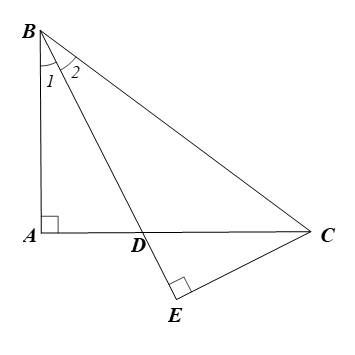\(\widehat {BAD} = \widehat {BEC} = 90^\circ \) và \(\widehat {{B_1}} = \widehat {{B_2}}\) (vì \(BD\) là tia phân giác của góc \(ABC)\)

Do đó  (g.g).

Suy ra: \(\frac{{BD}}{{AD}} = \frac{{BC}}{{EC}}\) (tỉ số cạnh tương ứng).

Do đó \(BD \cdot EC = AD \cdot BC.\)

c) Từ \(\frac{{DA}}{{DC}} = \frac{{AB}}{{BC}}\) suy ra \(\frac{{CD}}{{BC}} = \frac{{AD}}{{AB}}\)\(\left( 1 \right)\)

Vì  (câu b) nên \(\frac{{AD}}{{EC}} = \frac{{AB}}{{EB}},\) suy ra \(\frac{{AD}}{{AB}} = \frac{{EC}}{{EB}}\)\(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra: \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}.\)

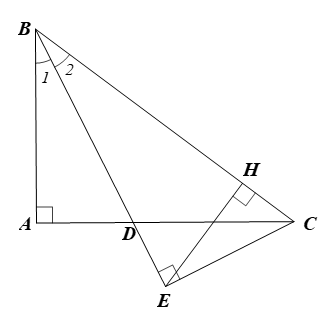
d) Tương tự câu b ta chứng minh được: ⦁  (g.g) nên \(\frac{{CH}}{{CE}} = \frac{{CE}}{{CB}}.\) Suy ra \(CH \cdot CB = C{E^2}\,\,\left( 3 \right)\) ⦁  (g.g) nên \(\frac{{ED}}{{EC}} = \frac{{CE}}{{BE}}.\) Suy ra \(ED \cdot EB = C{E^2}\left( 4 \right)\) Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra: \(CH \cdot HB = ED \cdot EB.\)

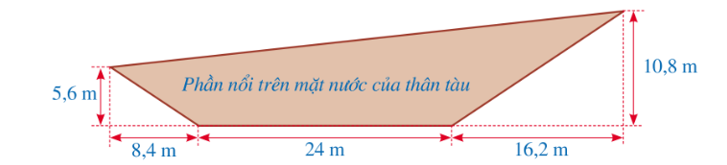
Giả sử mặt cắt dọc phần nổi trên mặt nước cả tàu thủy được mô tả như hình vẽ dưới đây:

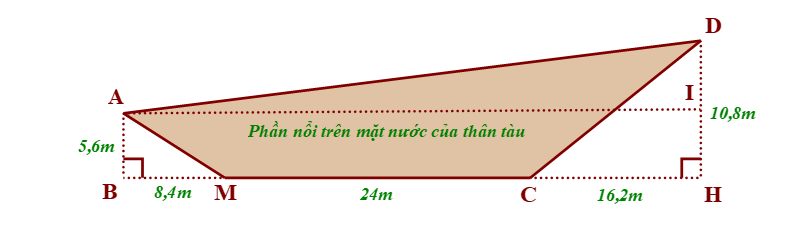
• Do tam giác \[ABM\] vuông tại \(B,\) nên theo định lí Pythagore ta có:

\[A{M^2} = A{B^2} + B{M^2} = 5,{6^2} + 8,{4^2} = 31,36 + 70,56 = 101,92\].

Suy ra \(AB = \sqrt {101,92} \,\,\left( {\rm{m}} \right).\)

• Do tam giác \(CDH\) vuông tại \(H,\) nên theo định lí Pythagore ta có:

\[C{D^2} = C{H^2} + D{H^2} = 16,{2^2} + 10,{8^2} = 262,44 + 116,64 = 379,08\]

Suy ra \(CD = \sqrt {379,08} \,\,\left( {\rm{m}} \right)\).

• Ta có \[AI = BH = BM + MC + CH = 8,4 + 24 + 16,2 = 48,6\] (m).

            \[DI = DH--HI = DH--AB = 10,8--5,6 = 5,2\] (m).

Do tam giác \[ADI\] vuông tại \[I,\] nên theo định lí Pythagore ta có:

\[A{D^2} = A{I^2} + D{I^2} = 48,{6^2} + 5,{2^2} = 2{\rm{ }}361,96 + 27,04 = 2{\rm{ }}389\]

Suy ra \(AD = \sqrt {2\,389} \,\,\left( {\rm{m}} \right)\).

• Chu vi tứ giác \(AMCD\) là:

\[AM + MC + CD + DA = \]\(\sqrt {101,92} + 24 + \sqrt {379,08} + \sqrt {2389} \approx 102,4\) (m).

Vậy chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó khoảng \[102,4{\rm{\;m}}{\rm{.}}\]