Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án (Đề 2)

a) Diện tích hình vuông \[EFGH\] là: \({x^2}\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

Diện tích hình chữ nhật \[ABCD\] là: \(2xy\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)

Phân thức biểu thị tỉ số diện tích hình vuông và diện tích hình chữ nhật \[ABCD\] là: \(\frac{{{x^2}}}{{2xy}} = \frac{x}{{2y}}.\)

Tử thức là \[x\,;\] mẫu thức là \[2y.\]

b) Giá trị của phân thức đó tại \[x = 2\,;{\rm{ }}y = 8\] là: \(\frac{2}{{2.8}} = \frac{2}{{16}} = \frac{1}{8}\).

a) Điều kiện xác định của biểu thức \[D\] là: \[3x \ne 0;{\rm{ }}x + 1 \ne 0;\]\(\frac{{2 - 4x}}{{x + 1}} \ne 0\)

• Xét \[3x \ne 0\] ta có \[x \ne 0.\]

• Xét \[x + 1 \ne 0\] ta có \[x \ne --1.\]

• Xét \(\frac{{2 - 4x}}{{x + 1}} \ne 0\) ta có \[2--4x \ne 0\] và \[x + 1 \ne 0,\] hay \(x \ne \frac{1}{2}\) và \[x \ne --1.\]

Vậy điều kiện xác định của biểu thức \[D\] là \(x \ne 0;\,\,x \ne - 1;\,\,x \ne \frac{1}{2}.\)

b) Với \(x \ne 0;\,\,x \ne - 1;\,\,x \ne \frac{1}{2},\) ta có:

\(D = \left( {\frac{{x + 2}}{{3x}} + \frac{2}{{x + 1}} - 3} \right):\frac{{2 - 4x}}{{x + 1}} - \frac{{3x - {x^2} + 1}}{{3x}}\)

\( = \frac{{\left( {x + 2} \right)\left( {x + 1} \right) + 2 \cdot 3x - 3 \cdot 3x\left( {x + 1} \right)}}{{3x \cdot \left( {x + 1} \right)}} \cdot \frac{{x + 1}}{{2 - 4x}} - \frac{{3x - {x^2} + 1}}{{3x}}\)

\( = \frac{{{x^2} + 2x + x + 2 + 6x - 9{x^2} - 9x}}{{3x\left( {x + 1} \right)}}.\frac{{x + 1}}{{2 - 4x}} - \frac{{3x - {x^2} + 1}}{{3x}}\)

\( = \frac{{ - 8{x^2} + 2}}{{3x\left( {x + 1} \right)}}.\frac{{x + 1}}{{2 - 4x}} - \frac{{3x - {x^2} + 1}}{{3x}}\)

\( = \frac{{2\left( {1 - 4{x^2}} \right) \cdot \left( {x + 1} \right)}}{{3x\left( {x + 1} \right) \cdot \left( {2 - 4x} \right)}} - \frac{{3x - {x^2} + 1}}{{3x}}\)

\( = \frac{{2\left( {1 - 2x} \right)\left( {1 + 2x} \right)}}{{3x \cdot 2\left( {1 - 2x} \right)}} - \frac{{3x - {x^2} + 1}}{{3x}}\)

\( = \frac{{1 + 2x}}{{3x}} - \frac{{3x - {x^2} + 1}}{{3x}} = \frac{{1 + 2x - 3x + {x^2} - 1}}{{3x}}\)

\( = \frac{{{x^2} - x}}{{3x}} = \frac{{x\left( {x - 1} \right)}}{{3x}} = \frac{{x - 1}}{3}\).

Vậy với \(x \ne 0;\,\,x \ne - 1;\,\,x \ne \frac{1}{2}\) thì \(D = \frac{{x - 1}}{3}.\)

c) Ta có \(\left( {2x - 1} \right)\left( {{x^2} + 1} \right) = 0\)

\(2x - 1 = 0\) hoặc \({x^2} + 1 = 0\) (vô nghiệm do \({x^2} + 1 > 0\) với mọi \(x)\)

\(x = \frac{1}{2}\)

Ta thấy \[x = \frac{1}{2}\] thỏa mãn điều kiện xác định.

Do đó, giá trị của biểu thức \[D\] tại \[x = \frac{1}{2}\] là: \(D = \frac{{\frac{1}{2} - 1}}{3} = \frac{{ - \frac{1}{2}}}{3} = - \frac{1}{6}.\)

Vậy \(D = - \frac{1}{6}\) khi \(\left( {2x - 1} \right)\left( {{x^2} + 1} \right) = 0.\)

Hướng dẫn giải

Gọi vận tốc của tàu hỏa thứ nhất là \(x\) (km/h) \(\left( {x > 0} \right).\)

Vận tốc của tàu hỏa thứ hai là \(x - 5\) (km/h).

Sau 4 giờ 48 phút \( = 4,8\) giờ thì tàu thứ nhất đi được quãng đường là: \(4,8x\) (km).

Vì tàu hỏa thứ hai khởi hành sau tàu hỏa thứ nhất 1 giờ 48 phút \( = 1,8\) giờ nên thời gian tàu hỏa thứ hai đã đi là \(4,8 - 1,8 = 3\) (giờ). Khi đó quãng đường tàu hỏa thứ hai đã đi là: \(3\left( {x - 5} \right)\) (km).

Vì ga Nam Định nằm trên đường từ Hà Nội đi TP Hồ Chí Minh và cách ga Hà Nội 87 km nên ta có phương trình:

\(4,8x = 3\left( {x - 5} \right) + 87\)

\(4,8x = 3x - 15 + 87\)

\(4,8x - 3x = 87 - 15\)

\(1,8x = 72\)

\(x = 40\) (thỏa mãn).

Vậy vận tốc của tàu hỏa thứ nhất là \(40\) km/h, vận tốc của tàu hỏa thứ hai là \(40 - 5 = 35\,\,\left( {{\rm{km/}}\,{\rm{h}}} \right).\)

a) Xét \(\Delta ABC\) vuông tại \(A,\) theo định lí Pytagore ta có: \(B{C^2} = A{B^2} + A{C^2} = {8^2} + {6^2} = 64 + 36 = 100\) Suy ra \(BC = \sqrt {100} = 10{\rm{\;cm}}.\) Vì \(BD\) là tia phân giác của góc \(ABC\) nên suy ra: \[\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}.\] b) Theo đề bài, \(CE \bot BD\) tại \(E\) nên \(\widehat {BEC} = 90^\circ .\) Xét \(\Delta ABD\) và \(\Delta EBC\) có:

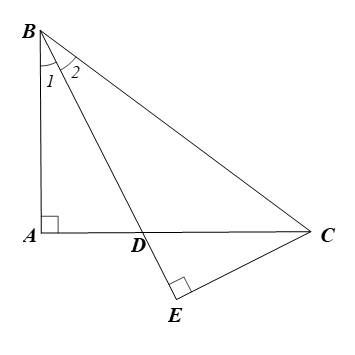\(\widehat {BAD} = \widehat {BEC} = 90^\circ \) và \(\widehat {{B_1}} = \widehat {{B_2}}\) (vì \(BD\) là tia phân giác của góc \(ABC)\)

Do đó  (g.g).

Suy ra: \(\frac{{BD}}{{AD}} = \frac{{BC}}{{EC}}\) (tỉ số cạnh tương ứng).

Do đó \(BD \cdot EC = AD \cdot BC.\)

c) Từ \(\frac{{DA}}{{DC}} = \frac{{AB}}{{BC}}\) suy ra \(\frac{{CD}}{{BC}} = \frac{{AD}}{{AB}}\)\(\left( 1 \right)\)

Vì  (câu b) nên \(\frac{{AD}}{{EC}} = \frac{{AB}}{{EB}},\) suy ra \(\frac{{AD}}{{AB}} = \frac{{EC}}{{EB}}\)\(\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra: \(\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}.\)

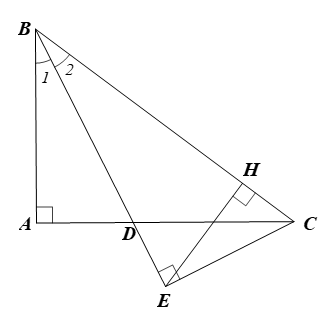
d) Tương tự câu b ta chứng minh được: ⦁  (g.g) nên \(\frac{{CH}}{{CE}} = \frac{{CE}}{{CB}}.\) Suy ra \(CH \cdot CB = C{E^2}\,\,\left( 3 \right)\) ⦁  (g.g) nên \(\frac{{ED}}{{EC}} = \frac{{CE}}{{BE}}.\) Suy ra \(ED \cdot EB = C{E^2}\left( 4 \right)\) Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra: \(CH \cdot HB = ED \cdot EB.\)