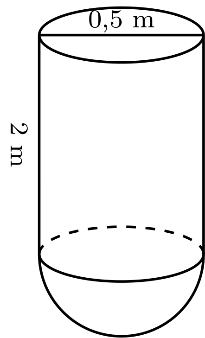
Trong các phát biểu sau, phát biểu nào đúng?
A. Mọi tứ giác luôn nội tiếp đường tròn.
B. Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \[90^\circ \].
C. Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng \[180^\circ \].
D. Tất cả các hình thang đều là tứ giác nội tiếp.
Quảng cáo
Trả lời:
Đáp án đúng là: C
Phát biểu “Tổng số đo hai góc đối của một tứ giác nội tiếp luôn bằng đây là dấu hiệu nhận biết của tứ giác nội tiếp.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
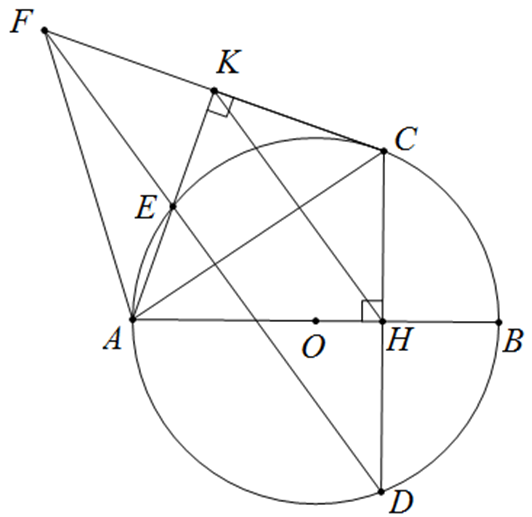
a) Vì \(CK \bot AK\) nên \(\widehat {AKC} = 90^\circ .\) Vì \(CH \bot AB\) tại \[H\] nên \(\widehat {AHC} = 90^\circ .\)
Gọi \(I\)là trung điểm \(AC\).
\(\Delta AKC\)có \(KI\) là trung tuyến ứng với cạnh huyền \(AC\) nên \(KI = OA = OC = \frac{1}{2}AC.\)
\(\Delta AHC\) có \(HI\) là trung tuyến ứng với cạnh huyền\(AC\) nên \(HI = IA = IC = \frac{1}{2}AC.\)
Do đó \(IA = IK = IC = IH.\)
Vậy bốn điểm
\(A,\,\,H,\,\,C,\,\,K\) cùng nằm trên cùng một đường tròn tâm \(I\) hay tứ giác \[AHCK\] nội tiếp.
b) Vì \[AHCK\] là tứ giác nội tiếp nên \(\widehat {CHK} = \widehat {CAK} = \widehat {CAE}\) (góc nội tiếp cùng chắn cung \[KC).\]
Lại có \[ADCE\]nội tiếp nên \(\widehat {CAE} = \widehat {CDE}\) (góc nội tiếp cùng chắn cung \[EC).\]
Từ đó suy ra \(\widehat {CHK} = \widehat {CDE}\) nên \(HK\,{\rm{//}}\,DE\) (đpcm).
Do \(HK\,{\rm{//}}\,DE\), mà \[H\] là trung điểm \[CD\] (quan hệ vuông góc của đường kính \[AB\] với dây \[CD\] tại \[H).\]
Suy ra \[HK\] là đường trung bình của tam giác \[CDF\] nên \[K\] là trung điểm \[FC\].
Tam giác \[AFC\] có \[AK\] là đường cao đồng thời cũng là trung tuyến.
Do đó tam giác \[CAF\]là tam giác cân tại \[K\] (đpcm).
c) Tam giác \[FAC\] cân tại \[A\] nên \[AF = AC.\]
Dễ thấy tam giác \[ACD\] cân tại \[A\] nên \[AC = AD\].
Từ đó suy ra \[AF = AD\] hay tam giác \[AFD\] cân tại \[A\], hạ \[DI \bot AF\] .
Ta có \({S_{AFD}} = \frac{1}{2}DI \cdot AF = \frac{1}{2}DI \cdot AC\).
Do \[AC\] không đổi nên \({S_{AFD}}\) lớn nhất khi và chỉ khi \[DI\] lớn nhất.
Trong tam giác vuông \[AID\] ta có:
\(ID \le AD = AC\) hay \({S_{AFD}} = \frac{1}{2}DI \cdot AF = \frac{1}{2}DI \cdot AC \le \frac{{A{C^2}}}{2}\).
Dấu xảy ra khi và chỉ khi \(I \equiv A\), khi đó \[\widehat {DAF} = 90^\circ \] nên tam giác \[ADF\] vuông cân tại \[A\], suy ra \(\widehat {EBA} = \widehat {EDA} = 45^\circ \) hay \[E\] là điểm chính giữa cung \[AB.\]
Vậy để diện tích tam giác \[ADF\] lớn nhất thì \[E\] là điểm chính giữa cung \[AB.\]
Câu 2
B. Tự luận
1. Sau khi điều tra về số học sinh trong \[100\] lớp học (đơn vị: học sinh), người ta có bảng tần số ghép nhóm như ở bảng sau:
|
Nhóm |
\[\left[ {36\,\,;\,\,38} \right)\] |
\[\left[ {38\,\,;\,\,40} \right)\] |
\[\left[ {40\,\,;\,\,42} \right)\] |
\[\left[ {42\,\,;\,\,44} \right)\] |
\[\left[ {44\,\,;\,\,46} \right)\] |
|
Tần số \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
a) Tìm tần số tương đối của mỗi nhóm đó.
b) Lập bảng tần số tương đối ghép nhóm và vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó.
2. Viết một số tự nhiên có chẵn có ba chữ số. Xét biến cố \(A:\) “Số tự nhiên là bội của 11”. Tính xác suất của biến cố \(A.\)
Lời giải
Hướng dẫn giải
1. a) Tần số tương đối của các nhóm lần lượt là: \[{f_1} = \frac{{20}}{{100}} \cdot 100\% = 20\% \]; \[{f_2} = \frac{{15}}{{100}} \cdot 100\% = 15\% \];
\[{f_3} = \frac{{25}}{{100}} \cdot 100\% = 25\% \];\[{f_4} = \frac{{30}}{{100}} \cdot 100\% = 30\% \]; \[{f_5} = \frac{{10}}{{100}} \cdot 100\% = 10\% \]
b) Bảng tần số tương đối của mỗi nhóm
|
Nhóm |
\[\left[ {36\,;\,38} \right)\] |
\[\left[ {38\,;40} \right)\] |
\[\left[ {40\,;42} \right)\] |
\[\left[ {42\,;\,44} \right)\] |
\[\left[ {44\,;46} \right)\] |
|
Tần số tương đối \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
Biểu đồ cột của mẫu số liệu ghép nhóm:
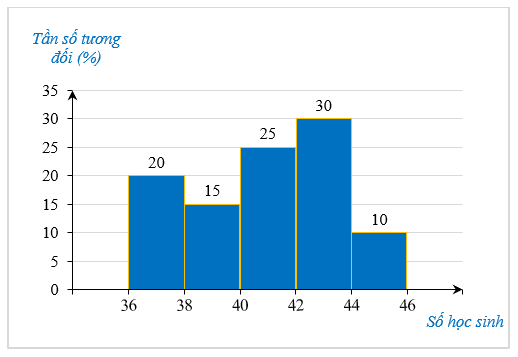
2. a) Số cách viết chữ số hàng trăm là 9 cách (các số từ 1 đến 9).
Số cách viết chữ số hàng chục là 10 cách (các số từ 0 đến 0).
Số cách viết các chữ hàng đơn vị để là số chẵn 5 cách (các số 0; 2; 4; 6; 8).
Vậy số phần tử của tập hợp \(\Omega \) là: \(9.10.5 = 450\) (phần tử)
b) Các số là bội của 11 là \(\left\{ {110\,;\,\,132\,;\,\,154\,;\,\, \ldots ;\,\,990} \right\}\).
Số phần tử tập hợp các số chia hết cho 11 gồm 3 chữ số chẵn là \(\left( {990 - 110} \right):22 + 1 = 41\).
Xác suất để số viết ra là số chia hết cho 11 là \(\frac{{41}}{{450}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Nón Huế là một hình nón có đường kính đáy bằng \[40\,\,{\rm{cm,}}\] độ dài đường sinh là \[30\,\,{\mathop{\rm cm}\nolimits} \]. Người ta lát mặt xung quanh hình nón bằng ba lớp lá khô. Tính d (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/blobid0-1741012868.png)