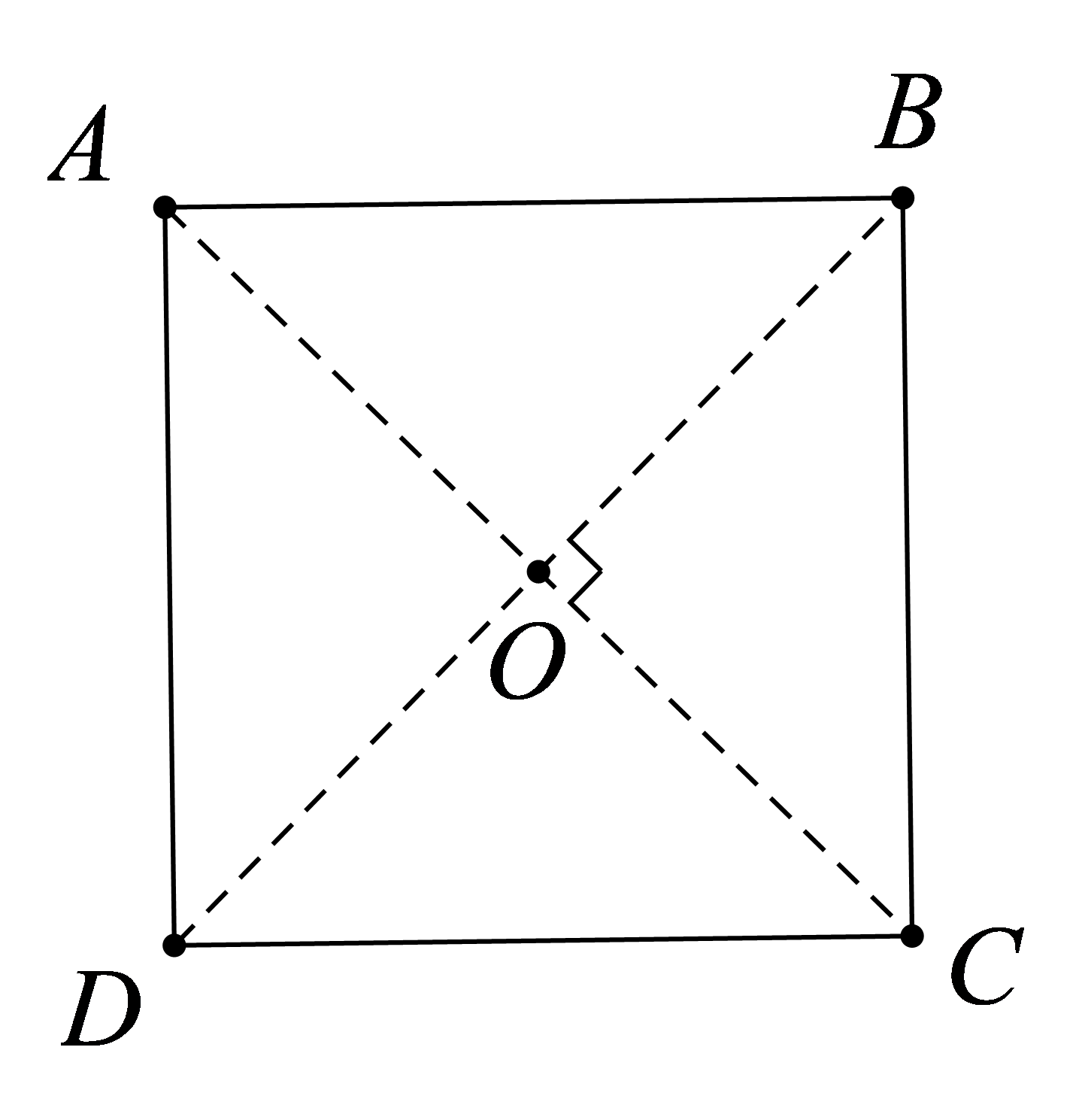Câu hỏi:
06/04/2025 251
Câu 8-10. (2,5 điểm)
Cho tam giác \[ABC\] nhọn có \[AB < AC\] nội tiếp đường tròn \[\left( {O;R} \right)\]. Các đường cao \[BE;\,\,CF\] của tam giác cắt nhau tại \[H\] \[\left( E \right.\] thuộc \[AC,\,\,F\]thuộc \[\left. {AB} \right).\]
a) Chứng minh tứ giác \[BFEC\] nội tiếp đường tròn.
Câu 8-10. (2,5 điểm)
a) Chứng minh tứ giác \[BFEC\] nội tiếp đường tròn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
![a) Chứng minh tứ giác \[BFEC\] nội tiếp đường tròn. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/04/36-1743951290.png)
a) Ta có \[BE,\,\,CF\] là hai đường cao của tam giác \[ABC\] nên \[\widehat {BFC} = \widehat {BEC} = 90^\circ .\]
Tam giác \[BCE\] vuông tại \[E\] nên \[B,\,\,C,\,\,E\] thuộc đường tròn đường kính \[BC.\]
Tam giác \[BFC\] vuông tại \[F\] nên \[B,\,\,C,\,\,F\] thuộc đường tròn đường kính \[BC.\]
Do đó \[B,\,\,C,\,\,E,\,\,F\] thuộc đường tròn đường kính \[BC.\]Hay tứ giác \[BFEC\] là tứ giác nội tiếp.
Câu hỏi cùng đoạn
Câu 2:
b) Kẻ đường kính \[AK\] của đường tròn \[\left( O \right)\]. Chứng minh \[AK\] vuông góc với \[EF\].
b) Kẻ đường kính \[AK\] của đường tròn \[\left( O \right)\]. Chứng minh \[AK\] vuông góc với \[EF\].
Lời giải của GV VietJack
Vì tứ giác \[BFEC\] nội tiếp nên \[\widehat {AEF} = \widehat {ABC}\], mà \[\widehat {AKC} = \widehat {ABC}\] nên \[\widehat {AKC} = \widehat {AEF}.\]
Xét đường tròn \[\left( O \right)\] có \(\widehat {ACK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên
\[\widehat {AKC} + \widehat {IAE} = 90^\circ \] hay \[\widehat {AEF} + \widehat {IAE} = 90^\circ .\]
Tam giác \[IAE\] vuông tại \[I\] nên \[AK \bot EF\] (đpcm).
Câu 3:
c) Giả sử \[BC\] cố định và \[A\] di chuyển trên cung lớn \[BC\] sao cho tam giác\[ABC\] luôn là tam giác nhọn. Xác định vị trí của điểm \[A\] để diện tích tam giác \[EAH\] lớn nhất. Tính giá trị lớn nhất đó theo \[R\] khi \[BC = R\sqrt 3 .\]
c) Giả sử \[BC\] cố định và \[A\] di chuyển trên cung lớn \[BC\] sao cho tam giác\[ABC\] luôn là tam giác nhọn. Xác định vị trí của điểm \[A\] để diện tích tam giác \[EAH\] lớn nhất. Tính giá trị lớn nhất đó theo \[R\] khi \[BC = R\sqrt 3 .\]
Lời giải của GV VietJack
Gọi \[M\] là giao điểm của \[BC\] và \[HK.\]
Vì \(\widehat {ABK},\,\,\widehat {ACK}\) đều là các góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \[\widehat {ABK} = 90^\circ ,\,\,\widehat {ACK} = 90^\circ \] hay \(AB \bot BK\,;\,\,AC \bot CK.\)
Vì \(AB \bot BK\) và \(AB \bot CF\) nên \[BK\,{\rm{//}}\,CF\] hay \[BK\,{\rm{//}}\,CH.\]
Vì \(AC \bot CK\) và \(AC \bot BE\) nên \[BE\,{\rm{//}}\,CK\] hay \[BH\,{\rm{//}}\,CK.\]
Xét tứ giác \(BHCK\) có \[BK\,{\rm{//}}\,CH\,;\,\,BH\,{\rm{//}}\,CK\] nên tứ giác \(BHCK\) là hình bình hành.
Suy ra hai đường chéo \(BC\) và \[HK\]cắt nhau tại trung điểm \[M\] của mỗi đường.
Xét tam giác \[AHK\] có \(O,\,\,M\) lần lượt là trung điểm của \(AK,\,\,HK\)
Suy ra \[OM\] là đường trung bình tam giác \[AHK\] nên \[AH = 2OM;\,\,OM\,{\rm{//}}\,AH.\]
Vì \[\Delta AEH\] vuông tại \[E\] nên \({S_{AEH}} = \frac{1}{2}AE \cdot EH \le \frac{1}{2} \cdot \frac{{A{E^2} + E{H^2}}}{2} = \frac{{A{H^2}}}{4} = O{M^2}. & \left( 1 \right)\)
Vì \[M\] là trung điểm của \(BC\) nên \[BM = \frac{{BC}}{2} = \frac{{R\sqrt 3 }}{2}.\]
Vì \[OM\,{\rm{//}}\,AH\] và \(AH \bot BC\) nên \(OM \bot BC.\)
Áp dụng định lí Pythagore vào \(\Delta OBM\) vuông tại \(M\) \(\left( {OM \bot BC} \right)\), ta có: \(O{B^2} = O{M^2} + B{M^2}\)
Khi đó \[O{M^2} = O{B^2} - B{M^2} = {R^2} - {\left( {\frac{{R\sqrt 3 }}{2}} \right)^2} = {R^2} - \frac{3}{4}{R^2} = \frac{{{R^2}}}{4}.\] Suy ra \(OM = \frac{R}{2}. & \left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \({S_{AEH}} \le \frac{{{R^2}}}{4}\).
Dấu xảy ra khi \[AE = EH\] nên \(\widehat {EAH} = 45^\circ \) hay \(\widehat {ACB} = 45^\circ \).
Vậy \[{\left( {{S_{AEH}}} \right)_{\max }} = \frac{{{R^2}}}{4}\] khi \[A\] thuộc cung lớn \[BC\] và \[\widehat {ACB} = 45^\circ .\]
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Thể tích khối gỗ là:
\[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {\left( {\frac{{90}}{2}} \right)^2} \cdot 75 \approx 158\,\,963\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\]
Vậy thể tích khối gỗ khoảng \[158\,\,963\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}.\]
Lời giải
a) Tổng số học sinh tham gia câu lạc bộ cờ vua là:
\(\left( {3 + 4} \right) + \left( {8 + 5} \right) + \left( {6 + 4} \right) + \left( {9 + 7} \right) = 46\) (học sinh).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận