Câu 4-5. (2,0 điểm) Biểu đồ dưới đây biểu diễn tỉ lệ về thời gian chạy cự li 100 mét của các học sinh lớp 9A.
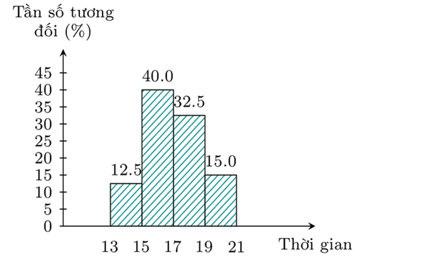
Biết rằng có 5 học sinh có thời gian chạy từ 13 giây đến dưới 15 giây.
a) Lập bảng tần số ghép nhóm tương ứng.
Câu 4-5. (2,0 điểm) Biểu đồ dưới đây biểu diễn tỉ lệ về thời gian chạy cự li 100 mét của các học sinh lớp 9A.

Biết rằng có 5 học sinh có thời gian chạy từ 13 giây đến dưới 15 giây.
a) Lập bảng tần số ghép nhóm tương ứng.
Quảng cáo
Trả lời:
a) Gọi \(n\) là tổng số học sinh của lớp 9A, ta có \(\frac{5}{n} \cdot 100\% = 12,5\% \).
Suy ra \(n = 40\) học sinh.
Ta có bảng phân bố tần số ghép nhóm như sau:
|
Thời gian (tính bằng giây) |
\(\left[ {13;15} \right)\) |
\(\left[ {15;17} \right)\) |
\(\left[ {17;19} \right)\) |
\(\left[ {19;21} \right)\) |
|
Tần số |
5 |
16 |
13 |
6 |
Câu hỏi cùng đoạn
Câu 2:
b) Bạn lớp trưởng cho rằng có trên 50% số học sinh của lớp có thời gian chạy nhanh hơn 17 giây. Nhận định đó đúng hay sai? Tại sao?
b) Bạn lớp trưởng cho rằng có trên 50% số học sinh của lớp có thời gian chạy nhanh hơn 17 giây. Nhận định đó đúng hay sai? Tại sao?
b) Tổng số học sinh chạy nhanh hơn 17 giây là 19 học sinh, đạt tỉ lệ \(\frac{{19}}{{40}} \cdot 100\% = 47,5\% .\)Do đó nhận định của bạn lớp trưởng là nhận định sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
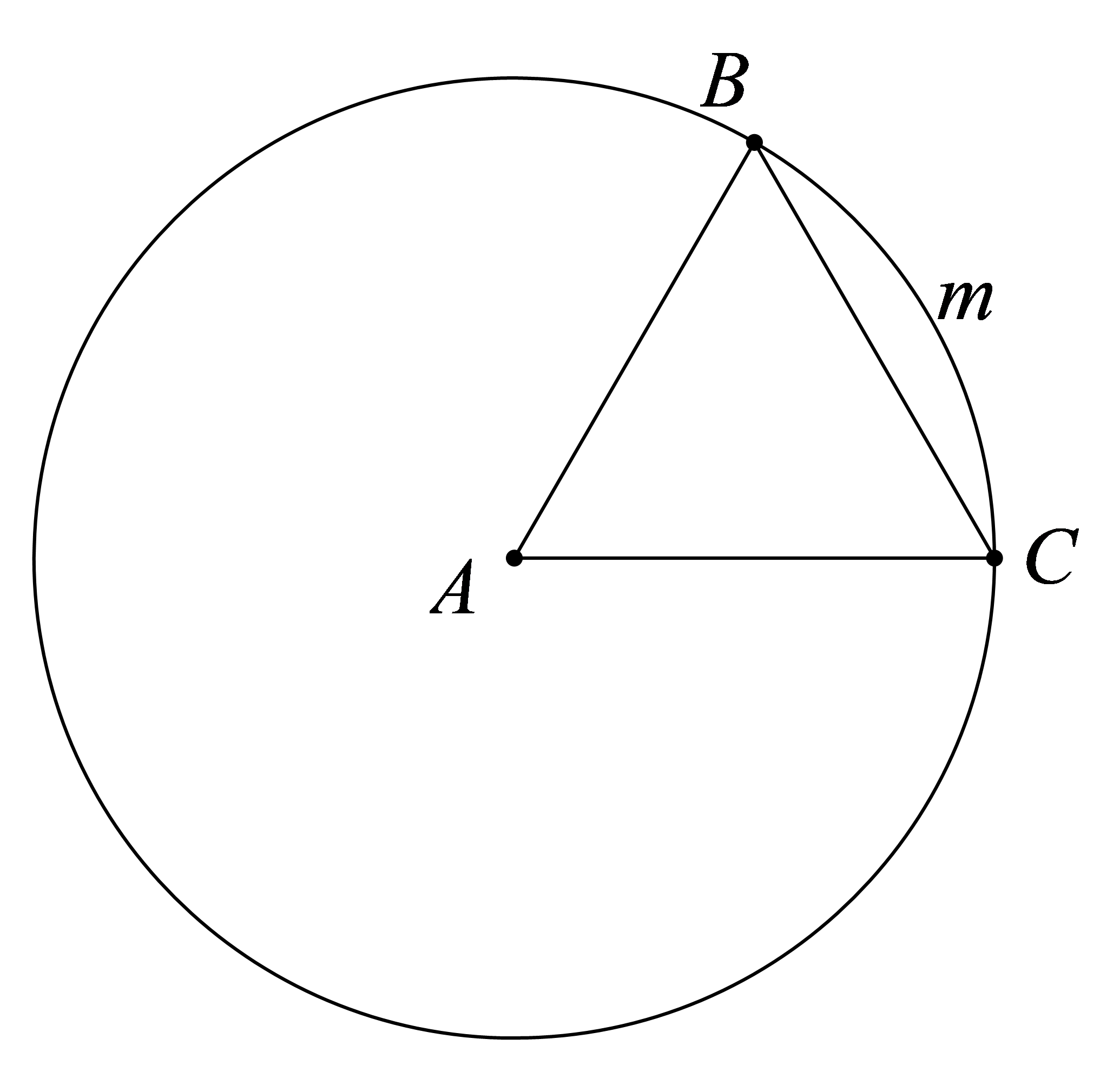
a) Tam giác \(ABC\) đều nên \(AB = AC\). Do đó \(C\) thuộc đường tròn \(\left( {A\,;\,\,AB} \right)\).
Xét đường tròn \(\left( {A\,;\,\,AB} \right)\), ta có: \(\widehat {BAC} = 60^\circ \) nên
Khi đó điểm \(B\) biến thành điểm \(C\) qua phép quay thuận chiều \(60^\circ \) tâm \(A\).b) Ta có: .
Khi đó điểm \({\rm{B}}\) biến thành điểm \({\rm{C}}\) qua phép quay ngược chiếu \(300^\circ \) tâm \({\rm{A}}\).
Lời giải
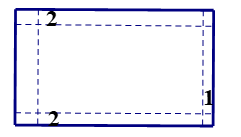
Nửa chu vi của vườn là \(\frac{{280}}{2} = 140\,\,\left( {\rm{m}} \right)\).
Gọi \(x\,\,\left( {\rm{m}} \right)\) là chiều dài của hình chữ nhật \(\left( {70 < {\rm{x}} < 140} \right).\)
Khi đó, chiều rộng của hình chữ nhật là: \(140 - x\,\,\left( {\rm{m}} \right)\).Mỗi bên để \(2{\rm{\;m}}\) làm lối đi nên chiều dài của đất để lại trồng trọt chỉ còn \(x - 4\,\,\left( {\rm{m}} \right)\) và chiêu rộng là: \(140 - x - 4 = 136 - x\,\,\left( {\rm{m}} \right)\).
Theo bài ra, ta có phương trình: \(\;\left( {x - 4} \right)\left( {136 - x} \right) = 4256\)
\(136x - {x^2} - 544 + 4x = 4256\)
\({x^2} - 140x + 4800 = 0\)
Ta có \(a = 1\,;\,\,b' = - 70\,;\,\,c = 4800\,;\,\,\Delta ' = 4900 - 4800 = 100 > 0\).
Do đó \(x = 60{\rm{\;}}\) (loại) hoặc \(x = 80\) (TMĐK).
Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là 80 m và 60 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.