Cho tam giác \(ABC\) đều như hình vẽ. Điểm \(B\) biến thành điểm nào?
• Phép phép quay thuận chiều \(60^\circ \) tâm \(A\).
• Phép phép quay ngược chiều \(300^\circ \) tâm \(A\).
Cho tam giác \(ABC\) đều như hình vẽ. Điểm \(B\) biến thành điểm nào?
• Phép phép quay thuận chiều \(60^\circ \) tâm \(A\).
• Phép phép quay ngược chiều \(300^\circ \) tâm \(A\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
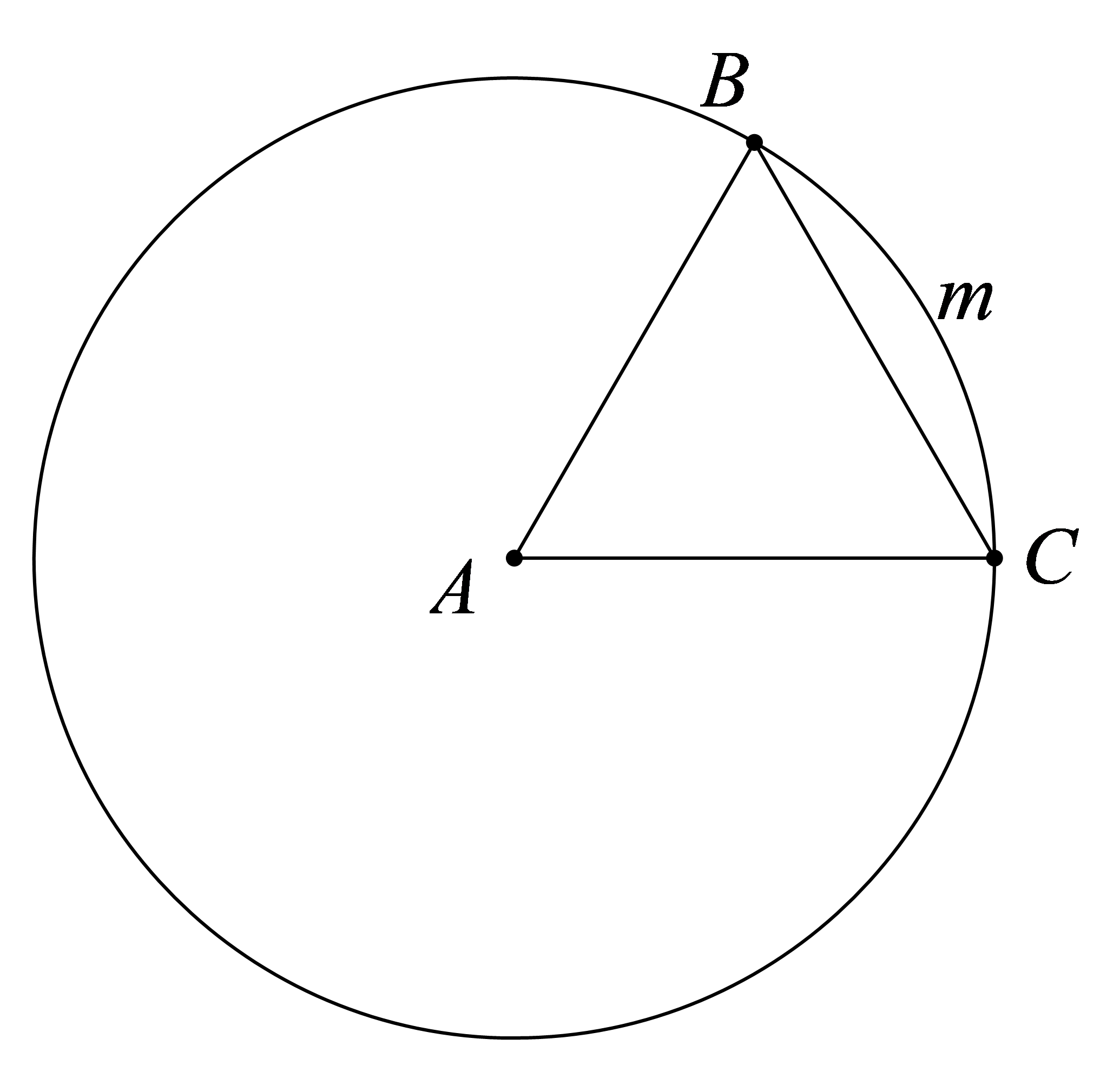
a) Tam giác \(ABC\) đều nên \(AB = AC\). Do đó \(C\) thuộc đường tròn \(\left( {A\,;\,\,AB} \right)\).
Xét đường tròn \(\left( {A\,;\,\,AB} \right)\), ta có: \(\widehat {BAC} = 60^\circ \) nên
Khi đó điểm \(B\) biến thành điểm \(C\) qua phép quay thuận chiều \(60^\circ \) tâm \(A\).b) Ta có: .
Khi đó điểm \({\rm{B}}\) biến thành điểm \({\rm{C}}\) qua phép quay ngược chiếu \(300^\circ \) tâm \({\rm{A}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
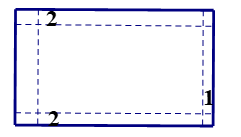
Nửa chu vi của vườn là \(\frac{{280}}{2} = 140\,\,\left( {\rm{m}} \right)\).
Gọi \(x\,\,\left( {\rm{m}} \right)\) là chiều dài của hình chữ nhật \(\left( {70 < {\rm{x}} < 140} \right).\)
Khi đó, chiều rộng của hình chữ nhật là: \(140 - x\,\,\left( {\rm{m}} \right)\).Mỗi bên để \(2{\rm{\;m}}\) làm lối đi nên chiều dài của đất để lại trồng trọt chỉ còn \(x - 4\,\,\left( {\rm{m}} \right)\) và chiêu rộng là: \(140 - x - 4 = 136 - x\,\,\left( {\rm{m}} \right)\).
Theo bài ra, ta có phương trình: \(\;\left( {x - 4} \right)\left( {136 - x} \right) = 4256\)
\(136x - {x^2} - 544 + 4x = 4256\)
\({x^2} - 140x + 4800 = 0\)
Ta có \(a = 1\,;\,\,b' = - 70\,;\,\,c = 4800\,;\,\,\Delta ' = 4900 - 4800 = 100 > 0\).
Do đó \(x = 60{\rm{\;}}\) (loại) hoặc \(x = 80\) (TMĐK).
Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là 80 m và 60 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Ta có bảng sau:
|
Lần 2 Lần 1 |
1 |
2 |
3 |
4 |
|
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
Không gian mẫu là:
\[\Omega = \left\{ {\left( {1\,,\,\,1} \right)\,;\,\,\left( {1\,,\,\,2} \right)\,;\,\,\left( {1\,,\,\,3} \right)\,;\,\,\left( {1\,,\,\,4} \right)\,;\,\,\left( {2\,,\,\,1} \right)\,;\,\,\left( {2\,,\,\,2} \right);{\rm{ }}\left( {2\,,\,\,3} \right);{\rm{ }}\left( {2\,,\,\,4} \right);{\rm{ }}\left( {3\,,\,\,1} \right)\,;\,\,\left( {3\,,\,\,2} \right)} \right.\,;\,\,\left( {3\,,\,\,3} \right)\,;\,\,\left( {3\,,\,\,4} \right)\,;{\rm{ }}\] \[\left. {\left( {4\,,\,\,1} \right);\,\,\left( {4\,,\,\,2} \right);\,\,\left( {4\,,\,\,3} \right);\,\,\left( {4\,,\,\,4} \right)} \right\}.\]
Do đó, không gian mẫu có 16 phần tử.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập