Câu 12-13. (1,5 điểm) Chú Hề trên sân khấu thường có trang phục như Hình a. Mũ của chú Hề có dạng hình nón. Có thể mô phỏng cấu tạo, kích thước chiếc mũ của chú Hề như Hình b.
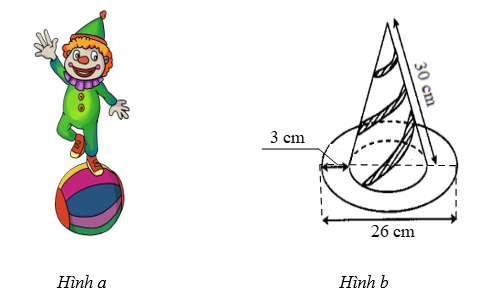
a) Để phủ kín mặt ngoài của chiếc mũ của chú Hề như Hình b cần bao nhiêu cemtimet vuông giấy màu (không tính phần mép dán, làm tròn kết quả đến hàng phần trăm).
Câu 12-13. (1,5 điểm) Chú Hề trên sân khấu thường có trang phục như Hình a. Mũ của chú Hề có dạng hình nón. Có thể mô phỏng cấu tạo, kích thước chiếc mũ của chú Hề như Hình b.

a) Để phủ kín mặt ngoài của chiếc mũ của chú Hề như Hình b cần bao nhiêu cemtimet vuông giấy màu (không tính phần mép dán, làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
a) Đường kính của hình nón là: \[26 - 2{\rm{ }}.{\rm{ }}3 = 20{\rm{ }}\left( {{\rm{cm}}} \right)\].
Bán kính \[r = \frac{{20}}{2} = 10{\rm{ }}\left( {{\rm{cm}}} \right)\].
Đường sinh là \[30{\rm{ cm}}\].
Vậy diện tích xung quanh của hình nón là:
\[{S_{xq}} = \pi rl = \pi \cdot 10 \cdot 30 = 300\pi {\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right) \approx 942,48{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Để phủ kín mặt ngoài chiếc mũ của chú hề, số giấy màu cần dùng là khoảng \[942,48{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\]
Câu hỏi cùng đoạn
Câu 2:
b) Hỏi thể tích phần có dạng hình nón của chiếc mũ chú hề ở Hình b bằng bao nhiêu centimét khối (làm tròn kết quả đến hàng phần trăm).
b) Hỏi thể tích phần có dạng hình nón của chiếc mũ chú hề ở Hình b bằng bao nhiêu centimét khối (làm tròn kết quả đến hàng phần trăm).
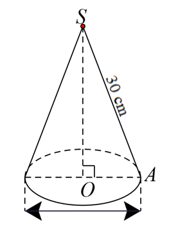
Bán kính của hình nón là: \(\frac{{26 - 3 \cdot 2}}{2} = 10{\rm{ }}\left( {{\rm{cm}}} \right)\).
Theo định lý Pythagore, ta có: \[S{A^2} = S{O^2} + O{A^2}\]
Suy ra \[SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{{30}^2} - {{10}^2}} = 20\sqrt 2 \,\,\left( {{\rm{cm}}} \right).\]
Chiều cao của hình nón \[h = SO = 20\sqrt 2 {\rm{ }}\left( {{\rm{cm}}} \right)\].
Thể tích phần có dạng hình nón của chiếc mũ hề là:
\[V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi \,.\,{10^2}\,{\rm{.}}\,{\rm{20}}\sqrt 2 \approx {\rm{2}}\,{\rm{961,92 }}\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\].
Vậy thể tích phần có dạng hình nón của chiếc mũ hề là \[{\rm{2}}\,{\rm{961,92 c}}{{\rm{m}}^{\rm{3}}}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
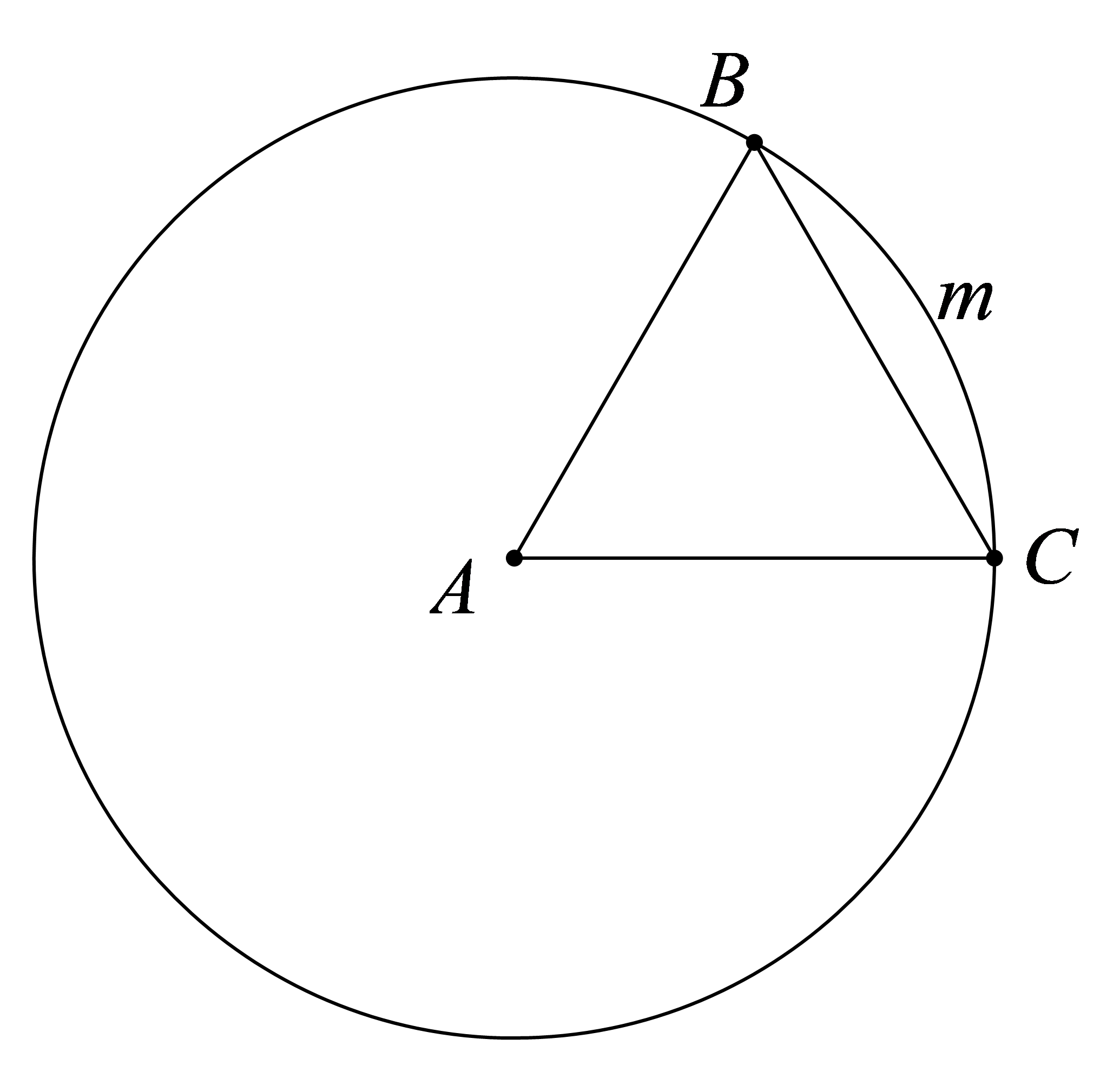
a) Tam giác \(ABC\) đều nên \(AB = AC\). Do đó \(C\) thuộc đường tròn \(\left( {A\,;\,\,AB} \right)\).
Xét đường tròn \(\left( {A\,;\,\,AB} \right)\), ta có: \(\widehat {BAC} = 60^\circ \) nên
Khi đó điểm \(B\) biến thành điểm \(C\) qua phép quay thuận chiều \(60^\circ \) tâm \(A\).b) Ta có: .
Khi đó điểm \({\rm{B}}\) biến thành điểm \({\rm{C}}\) qua phép quay ngược chiếu \(300^\circ \) tâm \({\rm{A}}\).
Lời giải
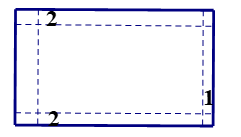
Nửa chu vi của vườn là \(\frac{{280}}{2} = 140\,\,\left( {\rm{m}} \right)\).
Gọi \(x\,\,\left( {\rm{m}} \right)\) là chiều dài của hình chữ nhật \(\left( {70 < {\rm{x}} < 140} \right).\)
Khi đó, chiều rộng của hình chữ nhật là: \(140 - x\,\,\left( {\rm{m}} \right)\).Mỗi bên để \(2{\rm{\;m}}\) làm lối đi nên chiều dài của đất để lại trồng trọt chỉ còn \(x - 4\,\,\left( {\rm{m}} \right)\) và chiêu rộng là: \(140 - x - 4 = 136 - x\,\,\left( {\rm{m}} \right)\).
Theo bài ra, ta có phương trình: \(\;\left( {x - 4} \right)\left( {136 - x} \right) = 4256\)
\(136x - {x^2} - 544 + 4x = 4256\)
\({x^2} - 140x + 4800 = 0\)
Ta có \(a = 1\,;\,\,b' = - 70\,;\,\,c = 4800\,;\,\,\Delta ' = 4900 - 4800 = 100 > 0\).
Do đó \(x = 60{\rm{\;}}\) (loại) hoặc \(x = 80\) (TMĐK).
Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là 80 m và 60 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.