Cho tam giác ABC vuông tại A có \(\frac{{AC}}{{AB}} = \frac{4}{3}\), đường cao AH = 4,8. Tính các cạnh AB, AC, BC, HB, HC.

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

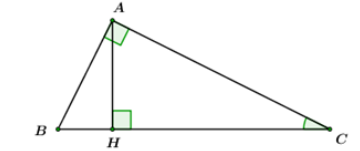
\(\frac{{AC}}{{AB}} = \frac{4}{3} \Rightarrow \frac{{AC}}{4} = \frac{{AB}}{3} = x \Rightarrow AC = 4x,AB = 3x\left( {x > 0} \right)\)

Áp dụng định lí Pytago ta có:

AB² + AC² = BC²

⇔ 9x² + 16x² = BC²

⇔ 25x² = BC²

Suy ra: BC = 5x

Áp dụng hệ thức lượng trong tam giác vuông:

AH.BC = AB.AC

⇔ 4,8.5x = 3x.4x

⇔ x = 2

Vậy AB = 6; AC = 8; BC = 10

Lại có AB² = HB.BC ⇒ \(HB = \frac{{A{B^2}}}{{BC}} = 3,6\)

HC =BC – HB = 10 – 3,6 = 6,4

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xem đáp án

Lời giải

Lời giải:

\(y = \frac{{2\sin x + \cos x}}{{\sin x + 2\cos x + 4}}\)

⇔ 2sinx + cosx = y.sinx + y.2cosx + 4y

⇔ (y.sinx – 2sinx) + (cosx.2y – cosx) = – 4y

⇔ sinx(y – 2) + cosy(2y – 1) = – 4y (*)

Điều kiện để (*) có nghiệm là: (y – 2)² + (2y – 1)² ≥ 16y²

⇔ 16y² – 8y + 5 ≤ 0

⇔ \(\frac{{ - 4 - \sqrt {71} }}{{11}} \le y \le \frac{{ - 4 + \sqrt {71} }}{{11}}\)

Vậy tập giá trị của y là \(\left[ {\frac{{ - 4 - \sqrt {71} }}{{11}};\frac{{ - 4 + \sqrt {71} }}{{11}}} \right]\)

Câu 2

Xem đáp án

Lời giải

Lời giải:

5³⁰⁰= (5²)¹⁵⁰= 25¹⁵⁰< 27¹⁵⁰= (3³)¹⁵⁰= 3⁴⁵⁰< 3⁴⁵³

Vậy 5³⁰⁰ < 3⁴⁵³

Câu 3