Câu hỏi:

19/08/2025 396

Cho tam giác ABC vuông tại A đường cao AH (H ∈ BC). Biết AB = 3 cm, AC = 4 cm.

a) Chứng minh ∆HBA ᔕ ∆ABC.

b) Tính độ dài đường cao AH.

c) Đường phân giác của \(\widehat {ABC}\) cắt AH, AC lần lượt tại M, N. Chứng minh MA.NA = MH.NC.

Xem lời giải

Câu hỏi trong đề: 10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

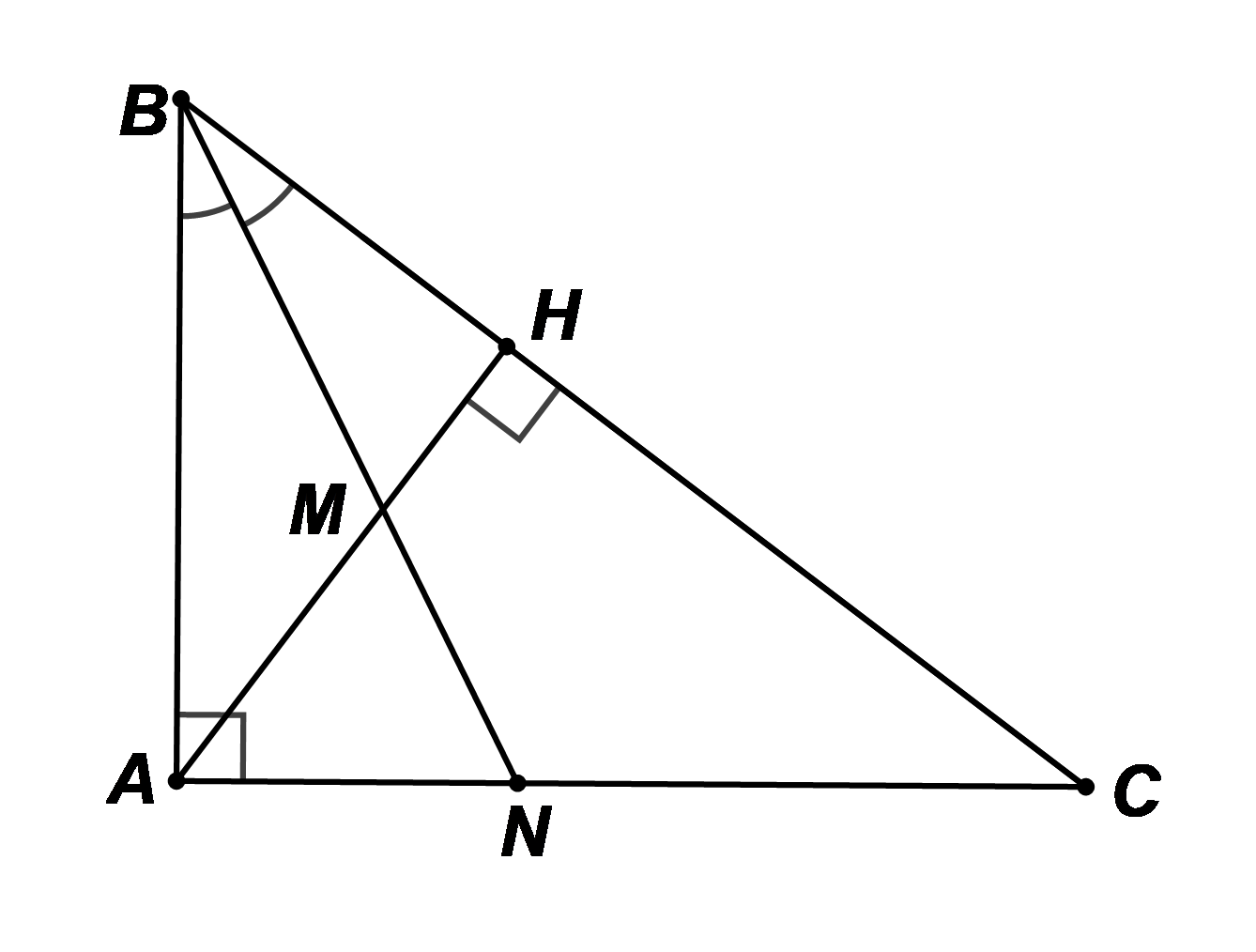
a) Chứng minh ∆HBA ᔕ ∆ABC. (ảnh 1)

a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có \[\widehat {HBA}\] chung

Do đó: ΔHBA ᔕ ΔABC (g.g).

b) Xét ΔABC vuông tại A, theo định lí Pythagore, ta có:

AB² + AC² = BC²

Suy ra \[BC = \sqrt {{3^2} + {4^2}} = 5\] (cm).

Vì ΔHBA ᔕ ΔABC (câu a) nên \[\frac{{BA}}{{BC}} = \frac{{HB}}{{AB}} = \frac{{HA}}{{AC}}\] (1)

Suy ra \[HA = \frac{{AB \cdot AC}}{{BC}} = \frac{{3 \cdot 4}}{5} = 2,4\] (cm).

c) Xét ΔABC có BN là phân giác nên \[\frac{{BA}}{{BC}} = \frac{{NA}}{{NC}}\] (2)

Xét ΔBHA có BM là phân giác nên \[\frac{{BH}}{{BA}} = \frac{{MH}}{{MA}}\] (3)

Từ (1), (2), (3) suy ra \[\frac{{NA}}{{NC}} = \frac{{MH}}{{MA}}\]

Suy ra MA.NA = MH.NC.

Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC là tam giác nhọn cân tại A. Kẻ hai đường cao BH và CK.

a) Chứng minh rằng đường tròn tâm O đường kính BC đi qua K và H.

b) Chứng minh rằng cung BH bằng cung CK.

c) Tính số đo cung KH nếu \[\widehat {BAC} = 40^\circ .\]

Xem đáp án

Lời giải

Lời giải:

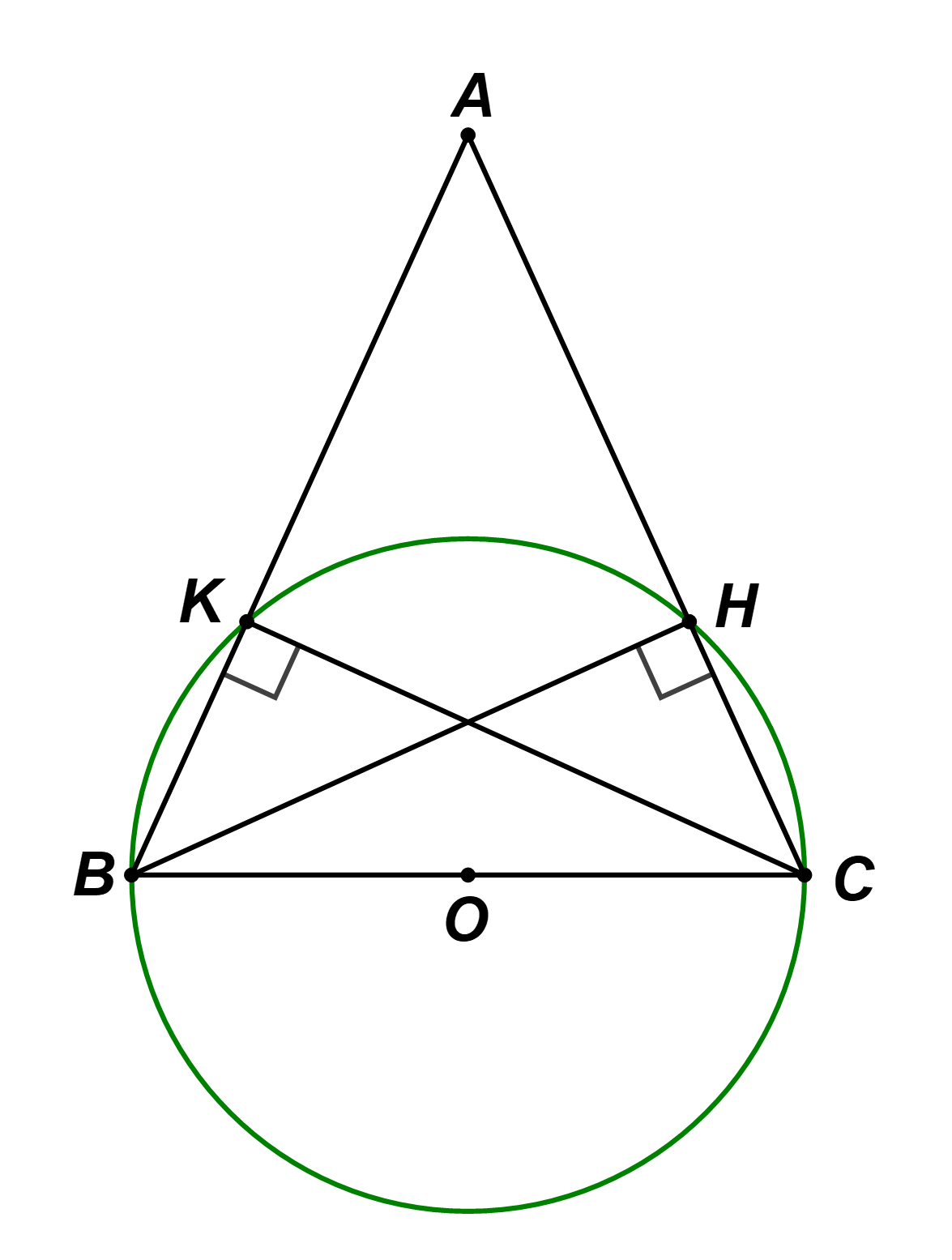
a) Chứng minh rằng đường tròn tâm O đường kính BC đi qua K và H. (ảnh 1)

a) Vì ΔBHC vuông tại H nên H nằm trên đường tròn đường kính BC

Do đó H nằm trên (O) đường kính BC.

Vì ΔBKC vuông tại K nên K nằm trên đường tròn đường kính BC

Do đó K nằm trên (O) đường kính BC.

b) Xét ΔKBC vuông tại K và ΔHCB vuông tại H có:

BC là cạnh chung

\[\widehat {KBC} = \widehat {HCB}\] (ΔABC cân tại A)

Do đó: ΔKBC = ΔHCB (cạnh huyền – góc nhọn)

Xét (O) có:

\[\widehat {KCB}\] là góc nội tiếp chắn cung BK

\[\widehat {HBC}\] là góc nội tiếp chắn cung HC

Mà \[\widehat {KCB} = \widehat {HBC}\] nên

c) Xét ∆ABH vuông tại H, ta có: \[\widehat {ABH} + \widehat {BAH} = 90^\circ \]

Suy ra \[\widehat {ABH} = 90^\circ - \widehat {BAH} = 90^\circ - 40^\circ = 50^\circ .\]

Lại có \(\widehat {KBH}\) là góc nội tiếp chắn cung KH của đường tròn (O)

Câu 2

Cho các tập hợp A = {0; 3; 4; 6}. Số tập hợp con gồm 2 phần tử của A là:

A. 12.

B. 8.

C. 10.

D. 6.

Xem đáp án

Lời giải

Lời giải:

Đáp án đúng là: D

Có 6 tập con gồm 2 phần tử của A là:

{0; 3}; {0; 4}; {0; 6}; {3; 4}; {3; 6}; {4; 6}.

Câu 3