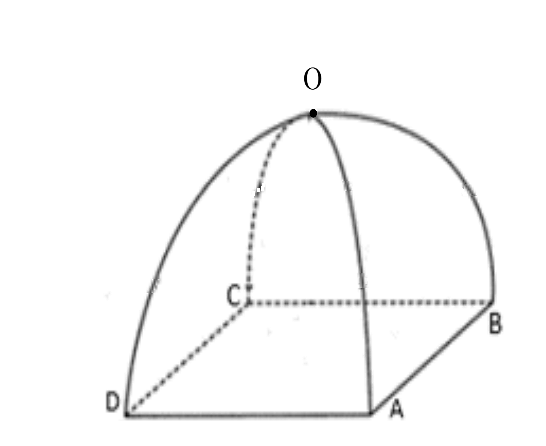
Trạm kiểm soát không quân đang theo dõi hai máy bay chiến đấu Su-30 và MiG-31. Giả sử trong không gian với hệ trục tọa độ \[Oxyz,\] đơn vị đo mỗi trục là \[1\,\,{\rm{km}}\] và xem mặt phẳng \(\left( {Oxy} \right)\) là mặt đất, tại cùng một thời điểm theo dõi ban đầu: máy bay chiến đấu Su-30 ở tọa độ \(A\left( {0\,;35\,;10} \right)\) bay theo hướng vectơ \({\vec v_1} = \left( {3\,;4\,;0} \right)\) với tốc độ không đổi \[900{\rm{ (km/h)}}\] và máy bay chiến đấu MiG-31 ở tọa độ \[B\left( {31;10;11} \right),\] bay theo hướng \[{\vec v_2} = \left( {5\,;12\,;0} \right)\] với tốc độ không đổi \[910{\rm{ (km/h)}}\]. Khu vực này có gió mạnh thổi với vận tốc \(80{\rm{ (km/h)}}\) theo hướng vectơ \(\vec u = \left( { - 3\,;0\,;4} \right),\) gió ảnh hưởng đến cả hai máy bay trong quá trình bay. Một khu vực không phận bị hạn chế bay đã được một quốc gia khác thiết lập, có dạng hình trụ với tâm đáy tại \(C\left( {178\,;430\,;0} \right)\), bán kính đáy \[7\,{\rm{km,}}\] trục vuông góc với mặt đất và chiều cao \[43\,{\rm{km,}}\] máy bay MiG-31 có nhiệm vụ bay vào khu vực không phận bị hạn chế để thăm dò. Tại thời điểm máy bay chiến đấu MiG-31 bay ra khỏi khu vực không phận bị hạn chế thì khoảng cách của 2 máy bay chiến đấu là bao nhiêu kilômét? (làm tròn kết quả đến hàng phần chục).

Trạm kiểm soát không quân đang theo dõi hai máy bay chiến đấu Su-30 và MiG-31. Giả sử trong không gian với hệ trục tọa độ \[Oxyz,\] đơn vị đo mỗi trục là \[1\,\,{\rm{km}}\] và xem mặt phẳng \(\left( {Oxy} \right)\) là mặt đất, tại cùng một thời điểm theo dõi ban đầu: máy bay chiến đấu Su-30 ở tọa độ \(A\left( {0\,;35\,;10} \right)\) bay theo hướng vectơ \({\vec v_1} = \left( {3\,;4\,;0} \right)\) với tốc độ không đổi \[900{\rm{ (km/h)}}\] và máy bay chiến đấu MiG-31 ở tọa độ \[B\left( {31;10;11} \right),\] bay theo hướng \[{\vec v_2} = \left( {5\,;12\,;0} \right)\] với tốc độ không đổi \[910{\rm{ (km/h)}}\]. Khu vực này có gió mạnh thổi với vận tốc \(80{\rm{ (km/h)}}\) theo hướng vectơ \(\vec u = \left( { - 3\,;0\,;4} \right),\) gió ảnh hưởng đến cả hai máy bay trong quá trình bay. Một khu vực không phận bị hạn chế bay đã được một quốc gia khác thiết lập, có dạng hình trụ với tâm đáy tại \(C\left( {178\,;430\,;0} \right)\), bán kính đáy \[7\,{\rm{km,}}\] trục vuông góc với mặt đất và chiều cao \[43\,{\rm{km,}}\] máy bay MiG-31 có nhiệm vụ bay vào khu vực không phận bị hạn chế để thăm dò. Tại thời điểm máy bay chiến đấu MiG-31 bay ra khỏi khu vực không phận bị hạn chế thì khoảng cách của 2 máy bay chiến đấu là bao nhiêu kilômét? (làm tròn kết quả đến hàng phần chục).

Quảng cáo
Trả lời:
Đáp án: 73,0.
Xác định các vectơ vận tốc:
Gọi \(\vec a:\) vectơ vận tốc của máy bay Su-30
\(\vec b:\) vectơ vận tốc của máy bay MiG-31
\(\vec c:\) vectơ vận tốc của gió
\({\vec u_1}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay Su-30
\({d_1}:\) đường thẳng quỹ đạo bay của máy bay Su-30
\({\vec u_2}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay MiG-31
\({d_2}:\) đường thẳng quỹ đạo bay của máy bay MiG-31
\(\left( T \right):\) mặt trụ có tâm \(C\left( {178\,;430\,;0} \right)\) bán kính \(r = 7.\)
\[\begin{array}{l}\left| {{{\vec v}_1}} \right| = \sqrt {{3^2} + {4^2} + {0^2}} = 5 \Rightarrow \vec a = \frac{{900}}{5}{{\vec v}_1} = \left( {540\,;720\,;0} \right)\\\left| {{{\vec v}_2}} \right| = 13 \Rightarrow \vec b = \frac{{910}}{{13}}{{\vec v}_2} = \left( {350\,;840\,;0} \right)\\\left| {\vec u} \right| = 5 \Rightarrow \vec c = \frac{{80}}{5}\vec u = \left( { - 48\,;0\,;64} \right)\\{{\vec u}_1} = \vec a + \vec c = \left( {492\,;720\,;64} \right) \Rightarrow {d_1}:\left\{ \begin{array}{l}x = 492t\\y = 35 + 720t\\z = 10 + 64t\end{array} \right.\\{{\vec u}_2} = \vec b + \vec c = \left( {302\,;840\,;64} \right) \Rightarrow {d_2}:\left\{ \begin{array}{l}x = 31 + 302t\\y = 10 + 840t\\z = 11 + 64t\end{array} \right.\\\left( T \right):{\left( {x - 178} \right)^2} + {\left( {y - 430} \right)^2} = {7^2}.\end{array}\]
Vì không phận cấm bay có độ cao \(43{\rm{ km}}\) nên MiG-31 vào trong không phận thì độ cao tối đa của máy bay là \(z \le 43 \Rightarrow 11 + 64t \le 43 \Leftrightarrow t \le 0,5.\)
Tìm giao điểm của \({d_2}\) và \(\left( T \right)\).
Xét phương trình: \({\left( {31 + 302t - 178} \right)^2} + {\left( {10 + 840t - 430} \right)^2} = 49\)
\( \Leftrightarrow 796804{t^2} - 794388t + 197960 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0,51 > 5\\t = 0,49 < 5\end{array} \right.\).
Dễ dàng nhận thấy MiG-31 đi vào không phận từ một điểm trên mặt trụ và đi ra tại một điểm trên đáy trên của khối trụ. Đáy trên của khối trụ nằm trong mặt phẳng có phương trình là \(z = 43\) hay \(t = 0,5.\)
Suy ra, sau \(0,5\) giờ MiG-31 nằm ở vị trí \(\left\{ \begin{array}{l}x = 31 + 302 \cdot 0,5 = 182\\y = 10 + 840 \cdot 0,5 = 430\\z = 43\end{array} \right. \Rightarrow M\left( {182\,;430\,;43} \right)\).
Su-30 nằm ở vị trí \(\left\{ \begin{array}{l}x = 492 \cdot 0,5 = 246\\y = 35 + 720 \cdot 0,5 = 395\\z = 42\end{array} \right. \Rightarrow N\left( {246\,;395\,;42} \right)\).
Khoảng cách giữa hai máy bay cần tìm là
\(MN = \sqrt {{{\left( {246 - 182} \right)}^2} + {{\left( {395 - 430} \right)}^2} + {{\left( {42 - 43} \right)}^2}} \approx 72,95 \approx 73,0\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 8.
Ta có \(AB = 2\sqrt 2 \Rightarrow AC = 4.\) Chọn hệ trục \(Oxy\) như hình vẽ.
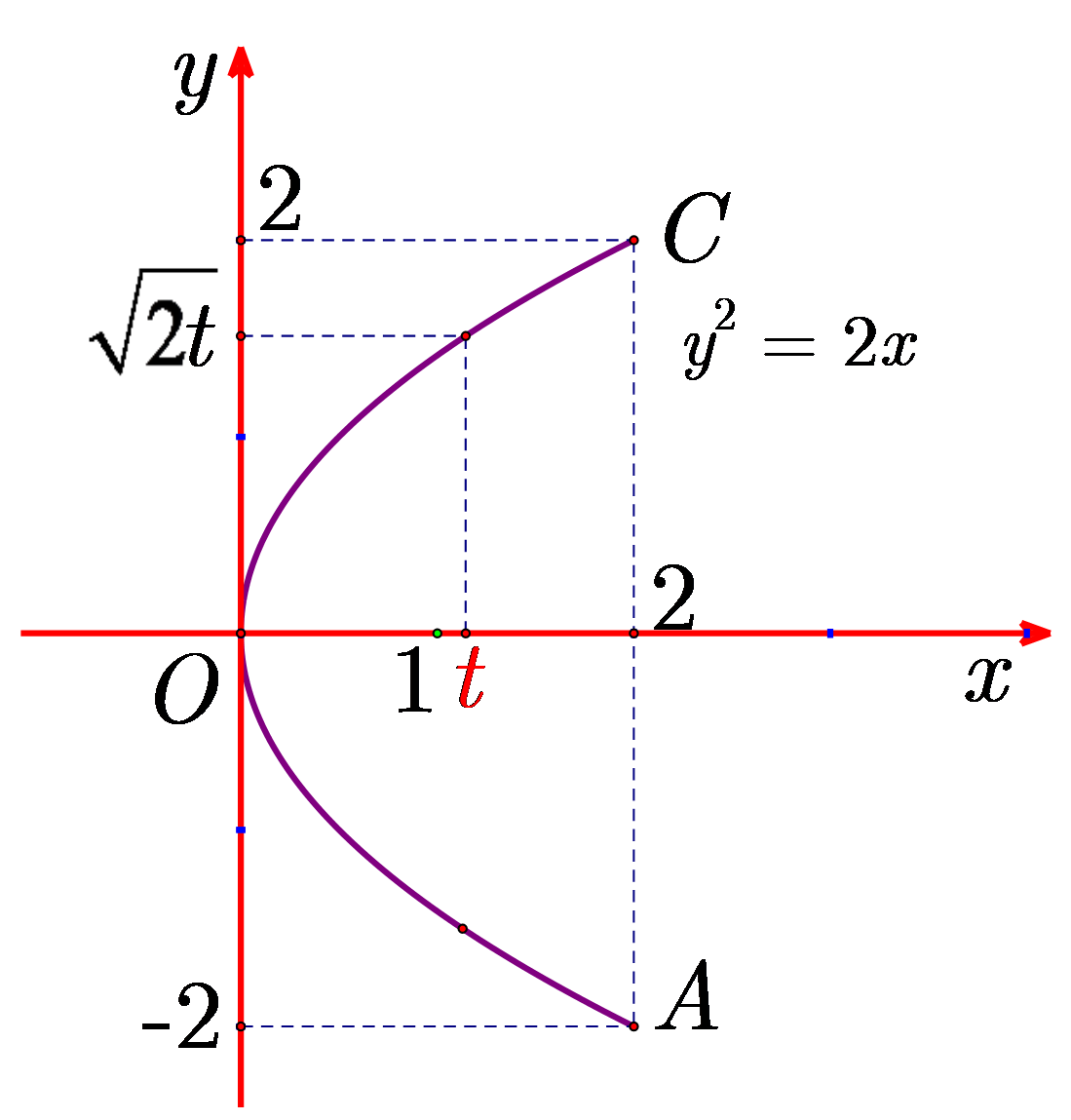
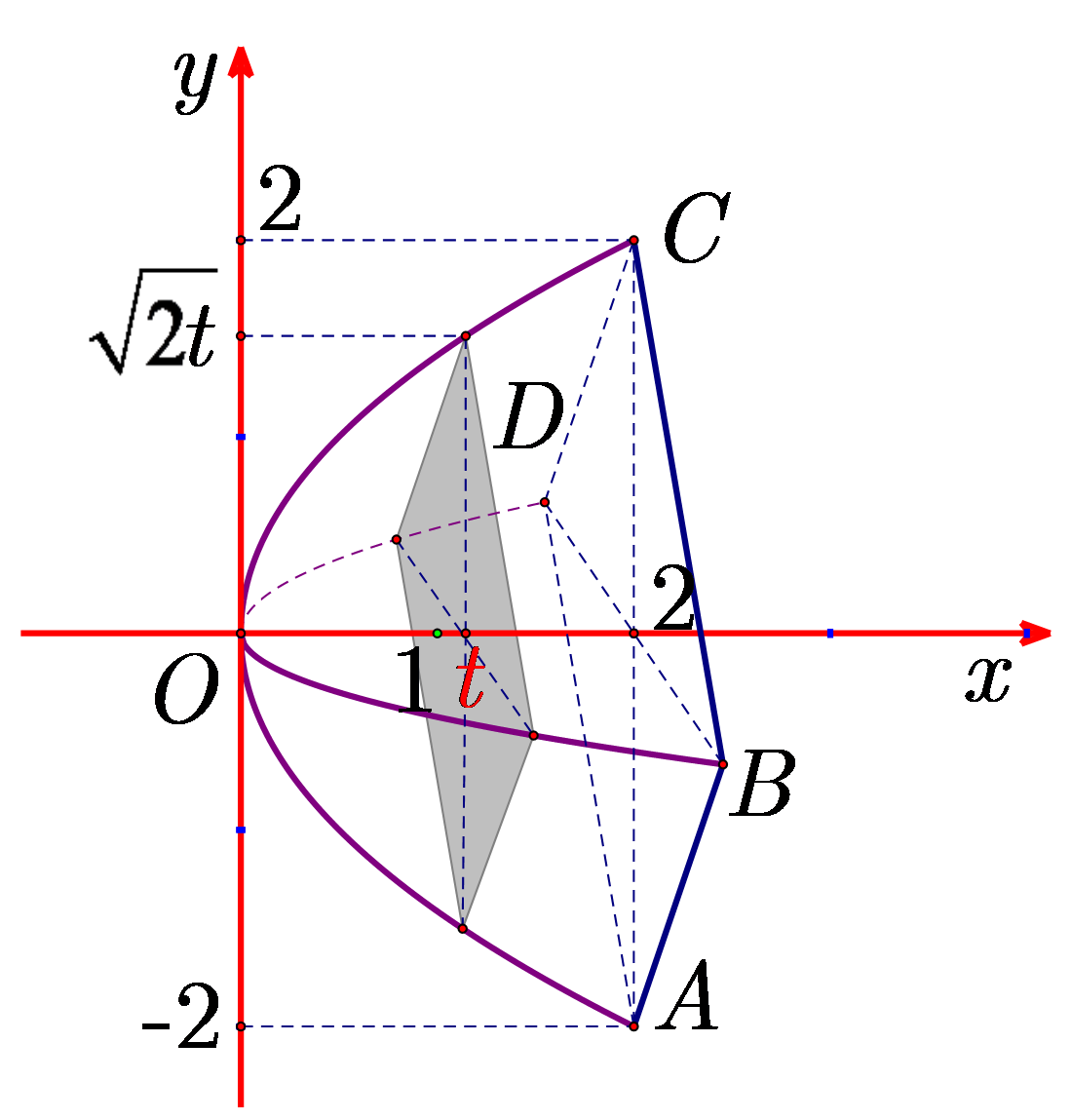
Khi đó, mặt cắt tại \(x = t\) là hình vuông có diện tích \(S\left( t \right) = \frac{1}{2}{\left( {2\sqrt {2t} } \right)^2} = 4t\).
Vậy thể tích của lều là \(V = \int\limits_0^2 {S\left( t \right){\rm{d}}t} = \int\limits_0^2 {4t{\rm{d}}t} = \left. {2{t^2}} \right|_0^2 = 8{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)
Lời giải
Đáp án: 12.
Lợi nhận hộ thu được trong một ngày là
\(L\left( x \right) = 300x - \left( {\frac{{23}}{{36}}{x^3} + {x^2} + 200} \right) = - \frac{{23}}{{36}}{x^3} - {x^2} + 300x - 200\).
\(L'\left( x \right) = - \frac{{23}}{{36}} \cdot 3{x^2} - 2x + 300 = 0 \Leftrightarrow - \frac{{23}}{{12}}{x^2} - 2x + 300 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 12\,\,\,\,\,\,\,\,\,\left( {{\rm{tm}}} \right)\\x = - \frac{{300}}{{23}}\,\,\,\left( {\rm{L}} \right)\end{array} \right.\).
Ta có \(L\left( 1 \right) = \frac{{3541}}{{36}};\,\,L\left( {12} \right) = 2152;\,\,L\left( {20} \right) = \frac{{2600}}{9}\). Suy ra \(\mathop {\max }\limits_{\left[ {1\,;\,20} \right]} L\left( x \right) = L\left( {12} \right) = 2152\).
Vậy để lợi nhuận đạt tối đa thì mỗi ngày hộ cần sản xuất 12 mét vải lụa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.