Câu hỏi:

23/05/2025 829

Một thành phố có ba loại phương tiện giao thông công cộng: xe buýt, tàu điện ngầm và taxi. Tỉ lệ sử dụng mỗi loại phương tiện đối với xe buýt \(40\% \), tàu điện ngầm \(35\% \), taxi \(25\% \). Tỉ lệ trễ giờ của xe buýt, tàu điện ngầm và taxi trong một tháng lần lượt là: \(20\% \), \(10\% \), \(5\% \). Anh Lộc là một người dân trong thành phố. Trong tháng đầu tiên, anh Lộc chọn một trong ba loại phương tiện trên để đi làm, sao cho xác suất chọn mỗi loại phương tiện đúng bằng tỉ lệ sử dụng phương tiện đó của người dân trong thành phố. Từ tháng thứ hai trở đi, cách anh Lộc chọn phương tiện đi làm phụ thuộc vào việc anh có bị trễ giờ trong tháng trước hay không: Nếu tháng trước anh Lộc không bị trễ giờ: Anh ấy tiếp tục sử dụng loại phương tiện mà anh đã đi trong tháng đó. Nếu tháng trước anh Lộc bị trễ giờ: Anh ấy sẽ chọn ngẫu nhiên một trong hai loại phương tiện còn lại để đi làm trong tháng tiếp theo, với xác suất chọn mỗi loại là \(50\% \). Xác suất để anh Lộc sử dụng taxi trong tháng thứ ba có dạng \(\frac{a}{b}\) (là phân số tối giản). Tính \(b - 2a\)?

Xem lời giải

Câu hỏi trong đề: Đề tham khảo ôn thi tốt nghiệp THPT môn Toán có đáp án (Đề số 24) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án: 5354.

Gọi \({A_i}\), \({B_i}\), \({C_i}\) lần lượt là các biến cố anh Lộc chọn xe buýt, tàu điện ngầm và taxi ở tháng thứ \(i\) với \(i = 1,2,3\). \(T\) là biến cố anh Lộc bị trễ.

Ta có \(P\left( {T|{A_i}} \right) = 0,2\), \(P\left( {T|{B_i}} \right) = 0,1\), \(P\left( {T|{C_i}} \right) = 0,05\).

Đặt \(P\left( {{A_i}} \right) = {x_i}\), \(P\left( {{B_i}} \right) = {y_i}\), \(P\left( {{C_i}} \right) = {z_i}\). Ta có sơ đồ cây như hình vẽ

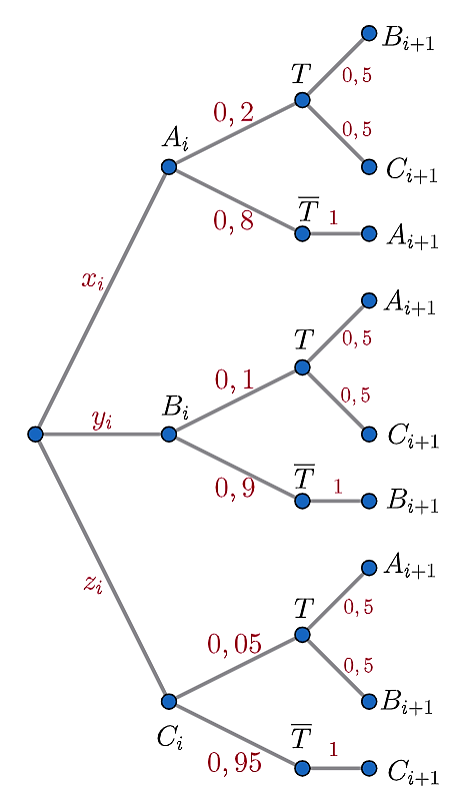
c (ảnh 1)

Từ sơ đồ cây ta có

\({x_{i + 1}} = P\left( {{A_{i + 1}}} \right) = 1 \cdot 0,8 \cdot {x_i} + 0,5 \cdot 0,1 \cdot {y_i} + 0,5 \cdot 0,05 \cdot {z_i}\)

\({y_{i + 1}} = P\left( {{B_{i + 1}}} \right) = 0,5 \cdot 0,2 \cdot {x_i} + 1 \cdot 0,9 \cdot {y_i} + 0,5 \cdot 0,05 \cdot {z_i}\)

\({z_{i + 1}} = P\left( {{C_{i + 1}}} \right) = 0,5 \cdot 0,2 \cdot {x_i} + 0,5 \cdot 0,1 \cdot {y_i} + 1 \cdot 0,95 \cdot {z_i}\)

Mà \({x_1} = 0,4\), \({y_1} = 0,35\) và \({z_1} = 0,25\).

Suy ra \({x_2} = 0,34375\), \({y_2} = 0,36125\), \({z_2} = 0,295\).

Vậy \({z_3} = \frac{{5323}}{{16000}} \Rightarrow a = 5323,b = 16000 \Rightarrow b - 2a = 5354\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một lều cắm trại có dạng như hình vẽ dưới, khung lều được tạo thành từ hai parabol giống nhau có chung đỉnh \[O\] và thuộc hai mặt phẳng vuông góc nhau (một parabol đi qua \[A,O,C\] và một parabol đi qua \[B,D,O\]), bốn chân tạo thành hình vuông \[ABCD\] có cạnh là \(2\sqrt 2 {\rm{ (m),}}\) chiều cao tính từ đỉnh lều là \(2{\rm{ (m)}}{\rm{.}}\) Biết mặt cắt của lều khi cắt bởi một mặt phẳng song song với mặt phẳng \(\left( {ABCD} \right)\) luôn là một hình vuông. Tính thể tích của lều (đơn vị là \({{\rm{m}}^3}\)).

Xem đáp án

Lời giải

Đáp án: 8.

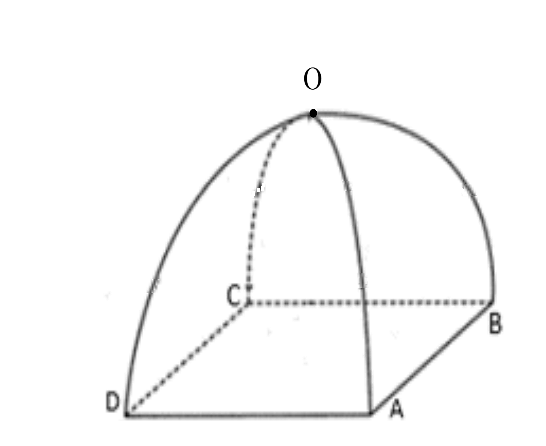
Ta có \(AB = 2\sqrt 2 \Rightarrow AC = 4.\) Chọn hệ trục \(Oxy\) như hình vẽ.

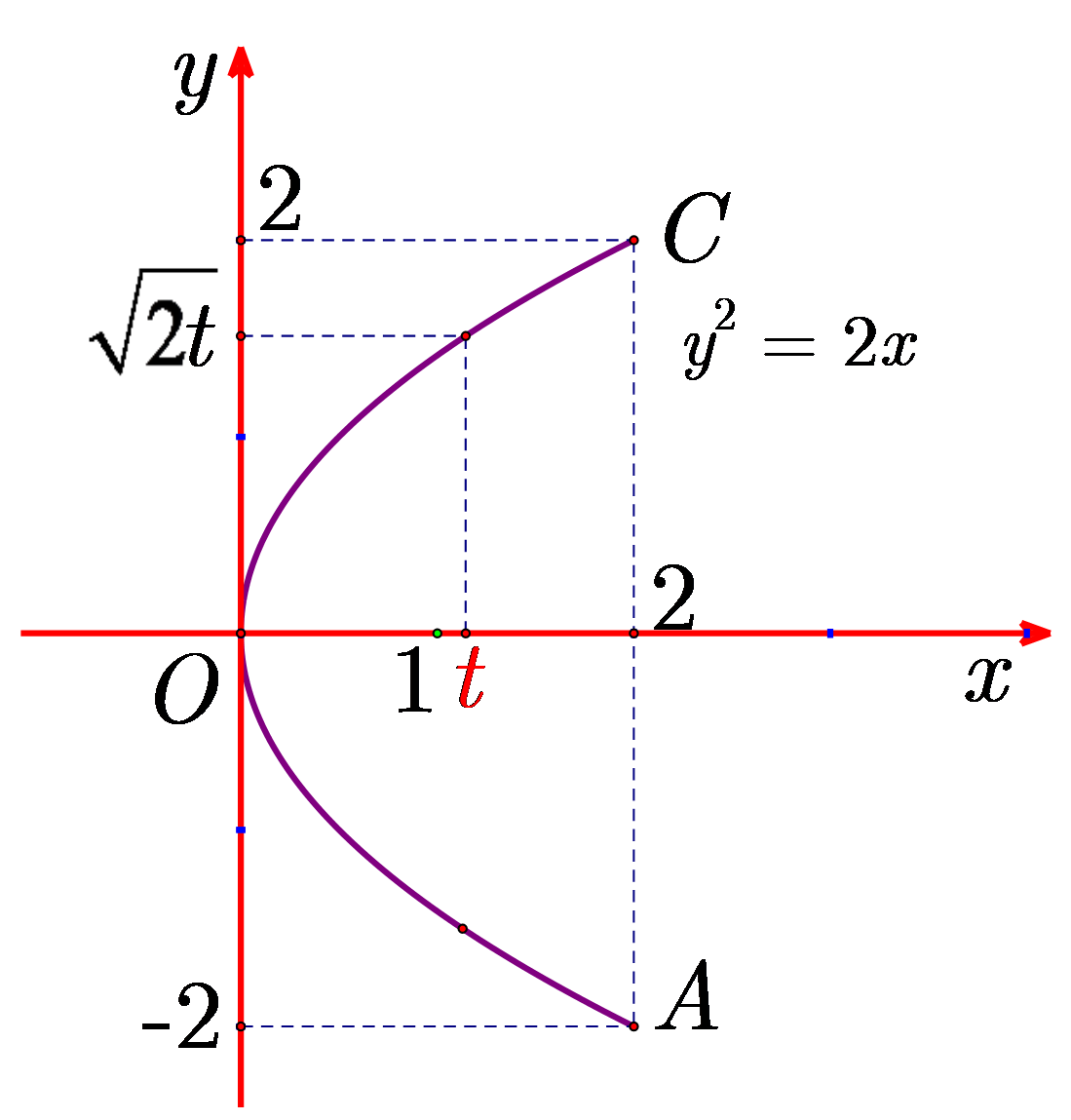
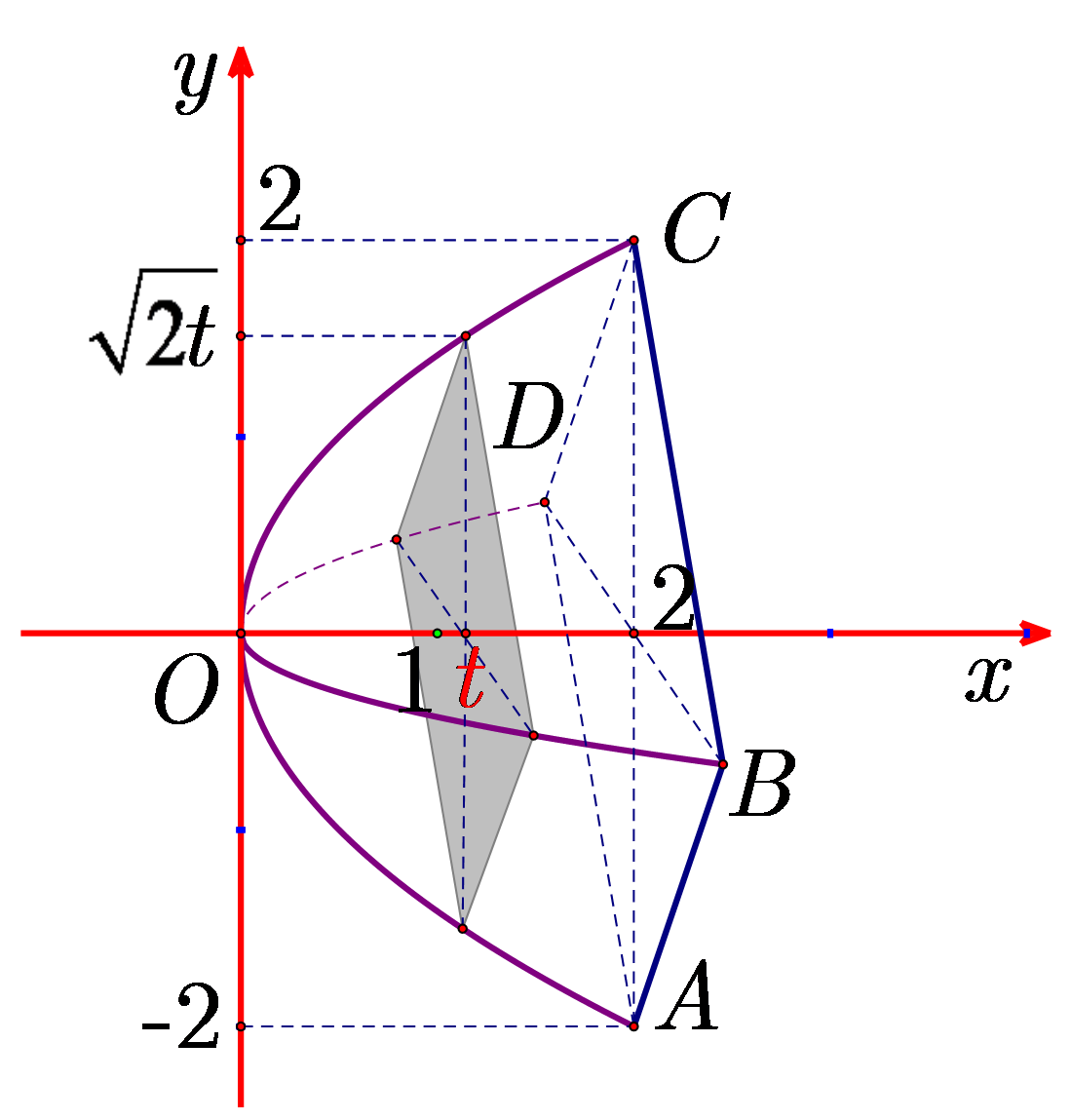
v (ảnh 2) v (ảnh 3)

Khi đó, mặt cắt tại \(x = t\) là hình vuông có diện tích \(S\left( t \right) = \frac{1}{2}{\left( {2\sqrt {2t} } \right)^2} = 4t\).

Vậy thể tích của lều là \(V = \int\limits_0^2 {S\left( t \right){\rm{d}}t} = \int\limits_0^2 {4t{\rm{d}}t} = \left. {2{t^2}} \right|_0^2 = 8{\rm{ }}\left( {{{\rm{m}}^3}} \right).\)

Câu 2

Trạm kiểm soát không quân đang theo dõi hai máy bay chiến đấu Su-30 và MiG-31. Giả sử trong không gian với hệ trục tọa độ \[Oxyz,\] đơn vị đo mỗi trục là \[1\,\,{\rm{km}}\] và xem mặt phẳng \(\left( {Oxy} \right)\) là mặt đất, tại cùng một thời điểm theo dõi ban đầu: máy bay chiến đấu Su-30 ở tọa độ \(A\left( {0\,;35\,;10} \right)\) bay theo hướng vectơ \({\vec v_1} = \left( {3\,;4\,;0} \right)\) với tốc độ không đổi \[900{\rm{ (km/h)}}\] và máy bay chiến đấu MiG-31 ở tọa độ \[B\left( {31;10;11} \right),\] bay theo hướng \[{\vec v_2} = \left( {5\,;12\,;0} \right)\] với tốc độ không đổi \[910{\rm{ (km/h)}}\]. Khu vực này có gió mạnh thổi với vận tốc \(80{\rm{ (km/h)}}\) theo hướng vectơ \(\vec u = \left( { - 3\,;0\,;4} \right),\) gió ảnh hưởng đến cả hai máy bay trong quá trình bay. Một khu vực không phận bị hạn chế bay đã được một quốc gia khác thiết lập, có dạng hình trụ với tâm đáy tại \(C\left( {178\,;430\,;0} \right)\), bán kính đáy \[7\,{\rm{km,}}\] trục vuông góc với mặt đất và chiều cao \[43\,{\rm{km,}}\] máy bay MiG-31 có nhiệm vụ bay vào khu vực không phận bị hạn chế để thăm dò. Tại thời điểm máy bay chiến đấu MiG-31 bay ra khỏi khu vực không phận bị hạn chế thì khoảng cách của 2 máy bay chiến đấu là bao nhiêu kilômét? (làm tròn kết quả đến hàng phần chục).

Xem đáp án

Lời giải

Đáp án: 73,0.

Xác định các vectơ vận tốc:

Gọi \(\vec a:\) vectơ vận tốc của máy bay Su-30

\(\vec b:\) vectơ vận tốc của máy bay MiG-31

\(\vec c:\) vectơ vận tốc của gió

\({\vec u_1}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay Su-30

\({d_1}:\) đường thẳng quỹ đạo bay của máy bay Su-30

\({\vec u_2}:\) vectơ chỉ phương của đường thẳng quỹ đạo bay của máy bay MiG-31

\({d_2}:\) đường thẳng quỹ đạo bay của máy bay MiG-31

\(\left( T \right):\) mặt trụ có tâm \(C\left( {178\,;430\,;0} \right)\) bán kính \(r = 7.\)

\[\begin{array}{l}\left| {{{\vec v}_1}} \right| = \sqrt {{3^2} + {4^2} + {0^2}} = 5 \Rightarrow \vec a = \frac{{900}}{5}{{\vec v}_1} = \left( {540\,;720\,;0} \right)\\\left| {{{\vec v}_2}} \right| = 13 \Rightarrow \vec b = \frac{{910}}{{13}}{{\vec v}_2} = \left( {350\,;840\,;0} \right)\\\left| {\vec u} \right| = 5 \Rightarrow \vec c = \frac{{80}}{5}\vec u = \left( { - 48\,;0\,;64} \right)\\{{\vec u}_1} = \vec a + \vec c = \left( {492\,;720\,;64} \right) \Rightarrow {d_1}:\left\{ \begin{array}{l}x = 492t\\y = 35 + 720t\\z = 10 + 64t\end{array} \right.\\{{\vec u}_2} = \vec b + \vec c = \left( {302\,;840\,;64} \right) \Rightarrow {d_2}:\left\{ \begin{array}{l}x = 31 + 302t\\y = 10 + 840t\\z = 11 + 64t\end{array} \right.\\\left( T \right):{\left( {x - 178} \right)^2} + {\left( {y - 430} \right)^2} = {7^2}.\end{array}\]

Vì không phận cấm bay có độ cao \(43{\rm{ km}}\) nên MiG-31 vào trong không phận thì độ cao tối đa của máy bay là \(z \le 43 \Rightarrow 11 + 64t \le 43 \Leftrightarrow t \le 0,5.\)

Tìm giao điểm của \({d_2}\) và \(\left( T \right)\).

Xét phương trình: \({\left( {31 + 302t - 178} \right)^2} + {\left( {10 + 840t - 430} \right)^2} = 49\)

\( \Leftrightarrow 796804{t^2} - 794388t + 197960 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0,51 > 5\\t = 0,49 < 5\end{array} \right.\).

Dễ dàng nhận thấy MiG-31 đi vào không phận từ một điểm trên mặt trụ và đi ra tại một điểm trên đáy trên của khối trụ. Đáy trên của khối trụ nằm trong mặt phẳng có phương trình là \(z = 43\) hay \(t = 0,5.\)

Suy ra, sau \(0,5\) giờ MiG-31 nằm ở vị trí \(\left\{ \begin{array}{l}x = 31 + 302 \cdot 0,5 = 182\\y = 10 + 840 \cdot 0,5 = 430\\z = 43\end{array} \right. \Rightarrow M\left( {182\,;430\,;43} \right)\).

Su-30 nằm ở vị trí \(\left\{ \begin{array}{l}x = 492 \cdot 0,5 = 246\\y = 35 + 720 \cdot 0,5 = 395\\z = 42\end{array} \right. \Rightarrow N\left( {246\,;395\,;42} \right)\).

Khoảng cách giữa hai máy bay cần tìm là

\(MN = \sqrt {{{\left( {246 - 182} \right)}^2} + {{\left( {395 - 430} \right)}^2} + {{\left( {42 - 43} \right)}^2}} \approx 72,95 \approx 73,0\).

Câu 3