Câu hỏi:
24/05/2025 8
Cho các hàm số
\(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) và \(g\left( x \right) = m{x^3} + n{x^2} + px + q\) \(\left( {a,b,c,d,m,n,p,q \in \mathbb{R}} \right)\).
Biết rằng đồ thị của hai hàm số \(f\left( x \right)\) và \(g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 4;{\rm{ }} - 1;{\rm{ }}4\) và \(f\left( 2 \right) = 2;{\rm{ }}g\left( 2 \right) = - 3\) (tham khảo hình vẽ bên dưới). Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và hai đường thẳng \(x = - 4;{\rm{ }}x = - 1\). Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và hai đường thẳng \(x = - 1;{\rm{ }}x = 4\). Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) (làm tròn kết quả đến hàng phần trăm).
Cho các hàm số
\(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) và \(g\left( x \right) = m{x^3} + n{x^2} + px + q\) \(\left( {a,b,c,d,m,n,p,q \in \mathbb{R}} \right)\).
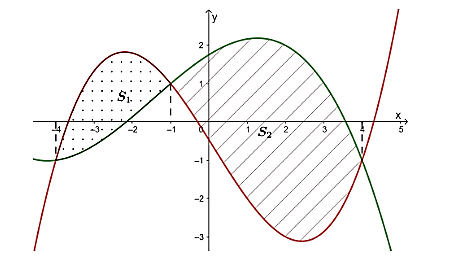
Biết rằng đồ thị của hai hàm số \(f\left( x \right)\) và \(g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 4;{\rm{ }} - 1;{\rm{ }}4\) và \(f\left( 2 \right) = 2;{\rm{ }}g\left( 2 \right) = - 3\) (tham khảo hình vẽ bên dưới). Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và hai đường thẳng \(x = - 4;{\rm{ }}x = - 1\). Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\left( x \right)\), \(y = g\left( x \right)\) và hai đường thẳng \(x = - 1;{\rm{ }}x = 4\). Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) (làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 0,26.
Vì \(f\left( x \right)\) và \(g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 4;{\rm{ }} - 1;{\rm{ }}4\).
Nên ta đặt hàm \(f\left( x \right) - g\left( x \right) = k\left( {x + 4} \right)\left( {x + 1} \right)\left( {x - 4} \right)\) (*).
Ta có \(f\left( 2 \right) = 2,{\rm{ }}g\left( 2 \right) = - 3\).
Thay \(x = 2\) vào (*) ta được \(f\left( 2 \right) - g\left( 2 \right) = k \cdot 6 \cdot 3 \cdot \left( { - 2} \right)\)\( \Leftrightarrow 2 - \left( { - 3} \right) = k \cdot \left( { - 36} \right) \Leftrightarrow k = \frac{{ - 5}}{{36}}\).
Suy ra \(f\left( x \right) - g\left( x \right) = - \frac{5}{{36}}\left( {x + 4} \right)\left( {x + 1} \right)\left( {x - 4} \right)\).
Khi đó, \({S_1} = \int\limits_{ - 4}^{ - 1} {\left| {f\left( x \right) - g\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - 4}^{ - 1} {\left| { - \frac{5}{{36}}\left( {x + 4} \right)\left( {x + 1} \right)\left( {x - 4} \right)} \right|{\rm{d}}x} = \frac{{65}}{{16}}\);
\({S_2} = \int\limits_{ - 1}^4 {\left| {f\left( x \right) - g\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - 1}^4 {\left| { - \frac{5}{{36}}\left( {x + 4} \right)\left( {x + 1} \right)\left( {x - 4} \right)} \right|{\rm{d}}x} = \frac{{6875}}{{432}}\).
Vậy tỉ số \(\frac{{{S_1}}}{{{S_2}}} = \frac{{351}}{{1375}} \approx 0,26\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết)
Đã bán 986
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
a) Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
a) Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Xem đáp án »
24/05/2025
39
Câu 4:
Tính hết năm \(2022\) diện tích rừng của thành phố \(X\) là \(140600\,{\rm{ha}}\), tỷ lệ che phủ rừng trên địa bàn thành phố đạt \(39,8\% \). Trong năm \(2022\) thành phố \(X\) trồng mới được \(1000\,{\rm{ha}}\). Giả sử diện tích rừng trồng mới của thành phố mỗi năm tiếp theo đều tăng \(6\% \) so với diện tích rừng trồng mới của năm liền trước. Sau ít nhất bao nhiêu năm thành phố có diện tích rừng đạt tỷ lệ che phủ \(45\% \)?
Tính hết năm \(2022\) diện tích rừng của thành phố \(X\) là \(140600\,{\rm{ha}}\), tỷ lệ che phủ rừng trên địa bàn thành phố đạt \(39,8\% \). Trong năm \(2022\) thành phố \(X\) trồng mới được \(1000\,{\rm{ha}}\). Giả sử diện tích rừng trồng mới của thành phố mỗi năm tiếp theo đều tăng \(6\% \) so với diện tích rừng trồng mới của năm liền trước. Sau ít nhất bao nhiêu năm thành phố có diện tích rừng đạt tỷ lệ che phủ \(45\% \)?
Xem đáp án »
24/05/2025
25
Câu 5:
Mỗi ngày bác Lan đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Lan trong \(20\) ngày được thống kê lại ở bảng sau:
\(\left[ {2,7;3,0} \right)\)
\(\left[ {3,0;3,3} \right)\)
\(\left[ {3,3;3,6} \right)\)
\(\left[ {3,6;3,9} \right)\)
\(\left[ {3,9;4,2} \right)\)
Số ngày
\(3\)
\(6\)
\(5\)
\(4\)
\(2\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm này có giá trị gần nhất với giá trị nào dưới đây?
Mỗi ngày bác Lan đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Lan trong \(20\) ngày được thống kê lại ở bảng sau:
|
\(\left[ {2,7;3,0} \right)\) |
\(\left[ {3,0;3,3} \right)\) |
\(\left[ {3,3;3,6} \right)\) |
\(\left[ {3,6;3,9} \right)\) |
\(\left[ {3,9;4,2} \right)\) |
|
|
Số ngày |
\(3\) |
\(6\) |
\(5\) |
\(4\) |
\(2\) |
Xem đáp án »
24/05/2025
21
Câu 6:
a) Xác suất \(P\left( A \right) = 0,01\) và \(P\left( {\overline A } \right) = 0,99\).
a) Xác suất \(P\left( A \right) = 0,01\) và \(P\left( {\overline A } \right) = 0,99\).
Xem đáp án »
24/05/2025
17
Câu 7:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + 2\) là:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.
Nguyên hàm của hàm số \(f\left( x \right) = 3{x^2} + 2\) là:
Xem đáp án »
24/05/2025
15
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 5)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận