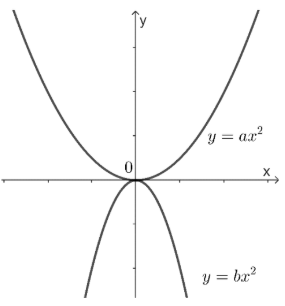
Trong mặt phẳng tọa độ Oxy, cho hai đồ thị hàm số có dạng như hình vẽ sau:Khẳng định nào sau đây là đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Vì đồ thị hàm số y = ax2 nằm phía trên trục hoành nên a > 0.
Vì đồ thị hàm số y = bx2 nằm phía dưới trục hoành nên b < 0.
Do đó b < 0 < a. Vậy ta chọn phương án D.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
Nhắn tin Zalo
Hỏi bài tập