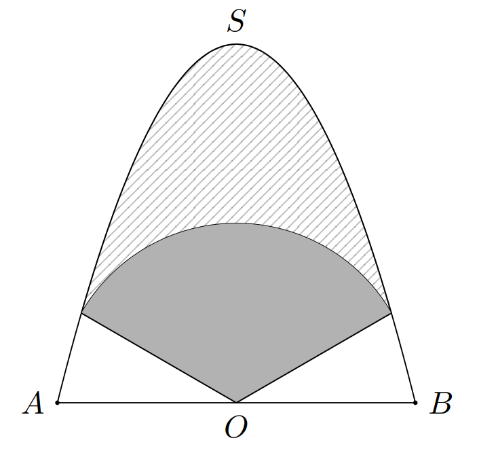
Để chuẩn bị quảng bá sản phẩm, người ta trang trí tấm pano dạng parabol như hình vẽ bên, biết \[OS = 8\,\,{\rm{m}}\], \[AB = 6\,\,{\rm{m}}\] với \[O\] là trung điểm của \[AB\]. Tấm pano được chia thành ba phần để trang trí với mức chi phí khác nhau: phần trên là phần kẻ sọc giá \(100\,000\) đồng/m², phần giữa là hình quạt tâm \[O\] bán kính \(3\,\,{\rm{m}}\) được tô đậm giá \(200\,000\) đồng/m², phần còn lại giá \(150\,000\) đồng/m². Tính tổng chi phí để trang trí tấm pano (đơn vị triệu đồng, kết quả làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
Chọn hệ trục \[Oxy\] với tia \[Ox\] trùng với tia \[OB\], tia \[Oy\] trùng với tia \[OS\] như hình vẽ.
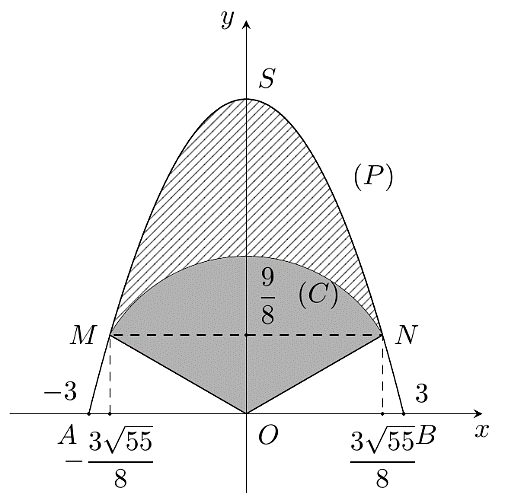
Khi đó ta có: \[A\left( { - 3;0} \right)\], \[B\left( {3;0} \right)\], \[S\left( {0;8} \right)\].
Suy ra parabol có phương trình là:
\[y = - \frac{8}{9}{x^2} + 8\] \[\left( P \right)\].
Rìa của hình quạt là cung tròn của đường tròn \[\left( C \right)\] có phương trình: \[{x^2} + {y^2} = 9 \Leftrightarrow y = \pm \sqrt {9 - {x^2}} \].
Hoành độ điểm \[N\] là nghiệm phương trình \[ - \frac{8}{9}{x^2} + 8 = \sqrt {9 - {x^2}} ,\,0 < x < 3\]\[ \Rightarrow x = \frac{{3\sqrt {55} }}{8}\].
Ta có \[{y_N} = - \frac{8}{9}{x_N}^2 + 8 = \frac{9}{8}\]. Suy ra \[N\left( {\frac{{3\sqrt {55} }}{8};\frac{9}{8}} \right)\].
Phương trình đường thẳng \[ON\]: \[y = \frac{3}{{\sqrt {55} }}x\].
Vì tấm pano đối xứng qua trục \[Oy\] nên ta có:
Diện tích phần kẻ sọc: \[{S_1} = 2 \cdot \int\limits_0^{\frac{{3\sqrt {55} }}{8}} {\left( { - \frac{8}{9}{x^2} + 8 - \sqrt {9 - {x^2}} } \right){\rm{d}}x} \approx 17,94\,\]m2.
Diện tích phần tô đậm: \[{S_2} = 2 \cdot \int\limits_0^{\frac{{3\sqrt {55} }}{8}} {\left( {\sqrt {9 - {x^2}} - \frac{3}{{\sqrt {55} }}x} \right)} \,{\rm{d}}x \approx 10,68\,\]m2.
Diện tích phần còn lại: \[S = \int\limits_{ - 3}^3 {\left( { - \frac{8}{9}{x^2} + 8} \right){\rm{d}}x} - \left( {{S_1} + {S_2}} \right) \approx 3,38\,\]m2.
Tổng chi phí để trang trí tấm pano là:
\[100{S_1} + 200{S_2} + 150S \approx 4\,440\] (nghìn đồng) \[ \approx 4,44\] (triệu đồng).
Đáp án: \(4,44\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
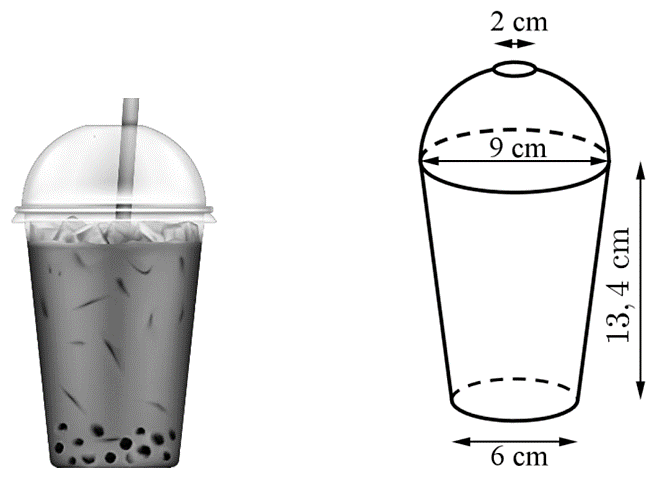
Chọn hệ trục \(Oxy\) (đơn vị trên trục là centimét) với trục \(Ox\) đi qua tâm của 2 đáy hình nón cụt và gốc tọa độ \(O\) trùng với tâm của đáy lớn như hình vẽ.
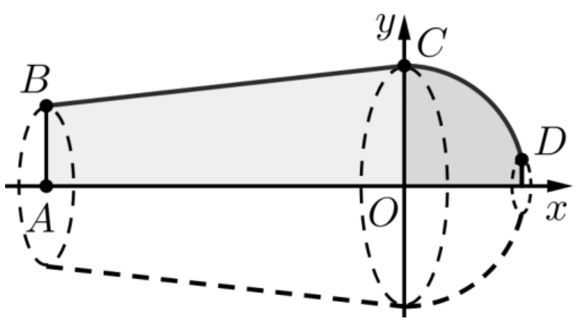
Khi đó toạ độ các điểm \(A,B,C\) lần lượt là \(A\left( { - 13,4;0} \right),B\left( { - 13,4;3} \right),C\left( {0;4,5} \right)\).
Gọi phương trình đường thẳng đi qua \(BC\) có dạng \(y = ax + b\).
Ta có hệ phương trình \(\left\{ \begin{array}{l} - 13,4a + b = 3\\0a + b = 4,5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{15}}{{134}}\\b = \frac{9}{2}\end{array} \right.\).
Phương trình đường thẳng BC là \(y = \frac{{15}}{{134}}x + \frac{9}{2}\).
Khi đó thể tích của phần thân ly trà sữa chưa bao gồm nắp là:
\({V_1} = \pi \int\limits_{ - 13,4}^0 {{{\left( {\frac{{15}}{{134}}x + \frac{9}{2}} \right)}^2}} {\rm{d}}x = \frac{{3819\pi }}{{20}}\,\,\,\,\left( 1 \right)\).
Điểm \(C,D\) thuộc đường tròn tâm \(O\left( {0;0} \right)\), bán kính \(R = 4,5\) có phương trình: \({x^2} + {y^2} = \frac{{81}}{4}\).
Thay \(y = 1\), ta được: \(x = \sqrt {\frac{{81}}{4} - 1} = \frac{{\sqrt {77} }}{2} \Rightarrow D\left( {\frac{{\sqrt {77} }}{2};1} \right)\). Suy ra \(y = \sqrt {\frac{{81}}{4} - {x^2}} \).
Khi đó thể tích nắp của ly trà sữa là: \[{V_2} = \pi \int\limits_0^{\frac{{\sqrt {77} }}{2}} {{{\left( {\sqrt {\frac{{81}}{4} - {x^2}} } \right)}^2}} {\rm{d}}x = \,\,\frac{{83\pi \sqrt {77} }}{{12}}\,\,\,\,\left( 2 \right)\].
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra thể tích bên trong của ly bao gồm cả thể tích của nắp là:
\(V = {V_1} + {V_2} = \frac{{3819\pi }}{{20}} + \frac{{83\pi \sqrt {77} }}{{12}} \approx 791\,\,{\rm{(c}}{{\rm{m}}^{\rm{3}}}{\rm{)}}\).
Đáp án: \(791\).
Câu 2
Một viên đạn được bắn thẳng đứng lên trên từ độ cao \(2\,\,{\rm{m}}\) với vận tốc tại thời điểm \(t\) cho bởi công thức \(v\left( t \right) = 100 - 9,8t\,\,\left( {{\rm{m/s}}} \right)\) (\(t = 0\) là thời điểm viên đạn được bắn lên). Tìm độ cao (tính theo \({\rm{km}}\)) của viên đạn so với mặt đất ở thời điểm 1 giây sau khi viên đạn đạt độ cao lớn nhất (làm tròn kết quả đến hàng phần trăm).
Một viên đạn được bắn thẳng đứng lên trên từ độ cao \(2\,\,{\rm{m}}\) với vận tốc tại thời điểm \(t\) cho bởi công thức \(v\left( t \right) = 100 - 9,8t\,\,\left( {{\rm{m/s}}} \right)\) (\(t = 0\) là thời điểm viên đạn được bắn lên). Tìm độ cao (tính theo \({\rm{km}}\)) của viên đạn so với mặt đất ở thời điểm 1 giây sau khi viên đạn đạt độ cao lớn nhất (làm tròn kết quả đến hàng phần trăm).
Lời giải
Gọi \(h\left( t \right)\) là độ cao (tính bằng mét) của viên đạn tại thời điểm \(t\) (tính bằng giây).
Ta có: \(h\left( t \right) = \int {v\left( t \right){\rm{d}}t = \int {\left( {100 - 9,8t} \right){\rm{d}}t = - 4,9{t^2} + 100t + C} } \).
Tại thời điểm \(t = 0\), ta có \(h\left( t \right) = 2 \Rightarrow C = 2\). Vậy \(h\left( t \right) = - 4,9{t^2} + 100t + 2\).
Ta có \(h'\left( t \right) = - 9,8t + 100;\) \(h'\left( t \right) = 0 \Leftrightarrow t = \frac{{500}}{{49}}\).
Bảng biến thiên:
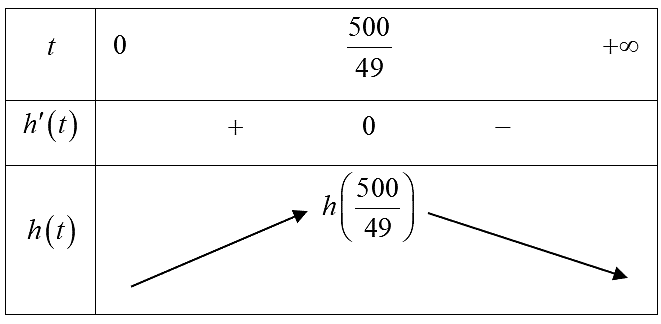
Từ bảng biến thiên suy ra viên đạn đạt độ cao lớn nhất tại thời điểm \(t = \frac{{500}}{{49}}\).
Do đó độ cao của viên đạn so với mặt đất ở thời điểm 1 giây sau khi viên đạn đạt độ cao lớn nhất là \(h\left( {\frac{{500}}{{49}} + 1} \right) \approx 507,3\,\,{\rm{m}} \approx 0,51\,\,{\rm{km}}\).
Đáp án: \(0,51\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.