Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai

Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Chị Linh bán được \(111\) chiếc áo gồm ba loại. Áo phông màu trắng giá \(100\) nghìn đồng một chiếc áo, áo phông màu đen giá \(80\) nghìn đồng một chiếc áo, áo phông màu xanh giá \(120\) nghìn đồng một chiếc. Biết rằng số tiền chị Linh bán được của ba loại áo phông là như nhau. Gọi \(x;y;z\) lần lượt là số áo phông chị Linh bán gồm áo phông màu trắng, áo phông màu đen và áo phông màu xanh.

a) Điều kiện của \(x;y;z\) là \(x,y,z \in {\mathbb{N}^*}\) và \(x,y,z < 111.\)

b) Phương trình biểu diễn tổng số áo chị Linh bán được là \(x + y + z = 111\).

c) Vì số tiền chị Linh bán được của mỗi loại áo phông là như nhau nên ta có tỉ lệ thức

\(\frac{x}{{\frac{1}{{80}}}} = \frac{y}{{\frac{1}{{100}}}} = \frac{z}{{\frac{1}{{120}}}}\).

d) Chị Linh bán số áo phông đen nhiều hơn số áo phông xanh là \(15\) chiếc áo.

Hướng dẫn giải

Gọi chiều dài và chiều rộng của thửa ruộng lần lượt là \(x;y{\rm{ }}\left( {x;y > 0} \right)\).

Theo đề bài, một thửa ruộng hình chữ nhật có hai cạnh tỉ lệ với \(3\) và \(5\) nên \(\frac{x}{5} = \frac{y}{3}\).

Mà chiều dài hơn chiều rộng \(40{\rm{ m}}\) nên \(x - y = 40\).

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\frac{x}{5} = \frac{y}{3} = \frac{{x - y}}{{5 - 3}} = \frac{{40}}{2} = 20\).

Suy ra \(x = 20.5 = 100{\rm{ }}\left( {\rm{m}} \right)\) và \(y = 20.3 = 60{\rm{ }}\left( {\rm{m}} \right)\).

Diện tích của thửa ruộng đó là: \(60.100 = 6{\rm{ }}000{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

Theo đề, \(1{\rm{ }}{{\rm{m}}^2}\) thu được số kilôgram thóc là: \(12:15 = 0,8{\rm{ }}\left( {{\rm{kg}}} \right)\).

Vậy cả thửa ruộng thu hoạch được số kilôgram thóc là: \(6{\rm{ }}000.0,8 = 4{\rm{ }}800{\rm{ }}\left( {{\rm{kg}}} \right)\).

Hướng dẫn giải

Đáp án đúng là: a) Đb) Sc) Đ d) Đ

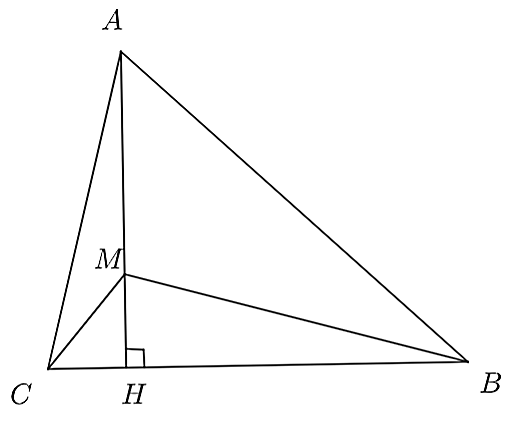
Do \(AB > AC\) (giả thiết)

Suy ra \(BH > HC\) (đường xiên lớn hơn thì hình chiếu lớn hơn)

Xét hai đường xiên \(MB\) và \(MC\) có \(BH > HC\) (cmt)

Do đó, \(MB > MC\) (hình chiếu lớn hơn thì đường xiên lớn hơn)

Ta có: \(BH\) là đường vuông góc với đường thẳng \(AH\).

Lại theo giả thiết điểm \(M\) nằm giữa hai điểm \(A\) và \(H\).

Nên \(MH < AH.\)

Suy ra \(BM < BA\) (hình chiếu lớn hơn thì đường xiên lớn hơn).

Do đó, \(BA > BM.\)