(1,0 điểm) Cho tam giác \(ABC\), trung tuyến \(BD\). Trên tia đối của tia \(DB\) lấy điểm \(E\) sao cho \(DE = BD\). Gọi \(P,Q\) lần lượt là điểm trên \(BE\) sao cho \(BP = PQ = QE\). Chứng minh:
a) \(CP,CQ\) cắt \(AB,AE\) tại trung điểm của \(AB,AE\).
b) \(CP\parallel AQ\) và \(CQ\parallel AP.\)
Quảng cáo
Trả lời:
Hướng dẫn giải
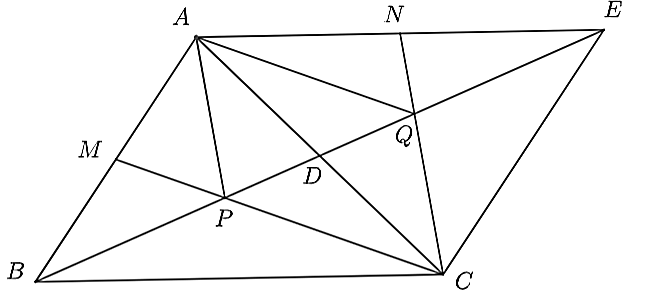
a) Gọi \(M,N\) lần lượt là trung điểm của \(AB,AE\).
Ta có: \(BP = PQ = QE\) và \(BD = DE\).
Mà \(BD = BP + PD;DE = QE + DQ\).
Suy ra \(PD = DQ\).
Hay \(D\) là trung điểm của \(PQ\).
Ta có: \(PD = \frac{1}{2}PQ\) hay \(PD = \frac{1}{2}BP\). Suy ra \(PD = \frac{1}{3}BD\)
Lại có \(BD\) là trung tuyến của \(\Delta ABC\).
Suy ra \(P\)là trọng tâm của \(\Delta ABC\).
Do đó, \(CP\) cắt \(AB\) tại trung điểm \(M.\)
Tương tự ta có: \(QD = \frac{1}{2}PQ = \frac{1}{2}QE\) hay \(QD = \frac{1}{3}ED\).
Do đó, \(Q\) là trọng tâm của tam giác \(AEC\).
Suy ra \(CQ\) cắt \(AE\) tại trung điểm \(N\).
b) Xét \(\Delta ADP\) và \(\Delta CDQ\) có:
\(AD = DC\) (gt)
\(\widehat {ADP} = \widehat {CDQ}\) (đối đỉnh)
\(PD = DQ\) (cmt)
Suy ra \(\Delta ADP = \Delta CDQ\) (c.g.c)
Suy ra \(\widehat {DAP} = \widehat {DCQ}\) (hai góc tương ứng).
Mà hai góc ở vị trí so le trong nên \(CQ\parallel AP.\)
Xét \(\Delta ADQ\) và \(\Delta CDP\) có:
\(AD = DC\) (gt)
\(\widehat {ADQ} = \widehat {CDP}\) (đối đỉnh)
\(PD = DQ\) (cmt)
Suy ra \(\Delta ADQ = \Delta CDP\) (c.g.c)
Suy ra \(\widehat {DAQ} = \widehat {DCP}\) (hai góc tương ứng).
Mà hai góc ở vị trí so le trong nên \(CP\parallel AQ\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Gọi chiều dài và chiều rộng của thửa ruộng lần lượt là \(x;y{\rm{ }}\left( {x;y > 0} \right)\).
Theo đề bài, một thửa ruộng hình chữ nhật có hai cạnh tỉ lệ với \(3\) và \(5\) nên \(\frac{x}{5} = \frac{y}{3}\).
Mà chiều dài hơn chiều rộng \(40{\rm{ m}}\) nên \(x - y = 40\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{5} = \frac{y}{3} = \frac{{x - y}}{{5 - 3}} = \frac{{40}}{2} = 20\).
Suy ra \(x = 20.5 = 100{\rm{ }}\left( {\rm{m}} \right)\) và \(y = 20.3 = 60{\rm{ }}\left( {\rm{m}} \right)\).
Diện tích của thửa ruộng đó là: \(60.100 = 6{\rm{ }}000{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Theo đề, \(1{\rm{ }}{{\rm{m}}^2}\) thu được số kilôgram thóc là: \(12:15 = 0,8{\rm{ }}\left( {{\rm{kg}}} \right)\).
Vậy cả thửa ruộng thu hoạch được số kilôgram thóc là: \(6{\rm{ }}000.0,8 = 4{\rm{ }}800{\rm{ }}\left( {{\rm{kg}}} \right)\).
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đb) Sc) Đ d) Đ
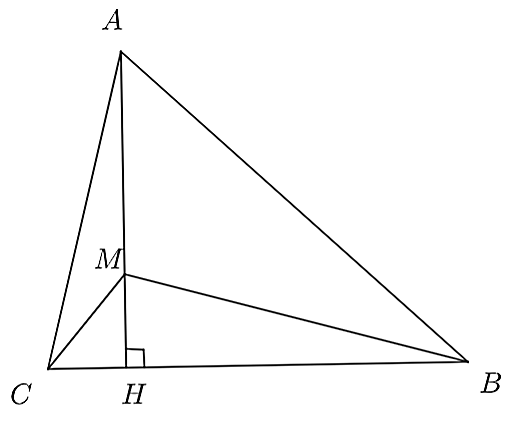
Do \(AB > AC\) (giả thiết)
Suy ra \(BH > HC\) (đường xiên lớn hơn thì hình chiếu lớn hơn)
Xét hai đường xiên \(MB\) và \(MC\) có \(BH > HC\) (cmt)
Do đó, \(MB > MC\) (hình chiếu lớn hơn thì đường xiên lớn hơn)
Ta có: \(BH\) là đường vuông góc với đường thẳng \(AH\).
Lại theo giả thiết điểm \(M\) nằm giữa hai điểm \(A\) và \(H\).
Nên \(MH < AH.\)
Suy ra \(BM < BA\) (hình chiếu lớn hơn thì đường xiên lớn hơn).
Do đó, \(BA > BM.\)
Câu 3
A. \(OA = \frac{2}{3}AM.\)
B. \(OM = \frac{1}{3}AM.\)
C. \(AO = \frac{2}{3}BN.\)
D. \(ON = \frac{1}{3}BN.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{1}{3}\) và \(\frac{2}{6}.\)
B. \(\frac{1}{3}\) và \(\frac{4}{5}\).
C. \(\frac{2}{6}\) và \(\frac{4}{5}\).
D. \(\frac{2}{6}\) và \(\frac{4}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.