B. TỰ LUẬN (3,0 điểm)
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Một thửa ruộng hình chữ nhật có chiều dài, chiều rộng tỉ lệ với \(5\) và \(3\). Biết chiều dài hơn chiều rộng là \(40{\rm{ m}}\). Người ta trồng lúa trên thửa ruộng đó, biết rằng cứ \(15{\rm{ }}{{\rm{m}}^2}\) thu hoạch được \(12{\rm{ kg}}\) thóc. Tính diện tích thửa ruộng và số kilôgram thóc thu hoạch được trên thửa ruộng đó.
Quảng cáo
Trả lời:
Hướng dẫn giải
Gọi chiều dài và chiều rộng của thửa ruộng lần lượt là \(x;y{\rm{ }}\left( {x;y > 0} \right)\).
Theo đề bài, một thửa ruộng hình chữ nhật có hai cạnh tỉ lệ với \(3\) và \(5\) nên \(\frac{x}{5} = \frac{y}{3}\).
Mà chiều dài hơn chiều rộng \(40{\rm{ m}}\) nên \(x - y = 40\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{5} = \frac{y}{3} = \frac{{x - y}}{{5 - 3}} = \frac{{40}}{2} = 20\).
Suy ra \(x = 20.5 = 100{\rm{ }}\left( {\rm{m}} \right)\) và \(y = 20.3 = 60{\rm{ }}\left( {\rm{m}} \right)\).
Diện tích của thửa ruộng đó là: \(60.100 = 6{\rm{ }}000{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Theo đề, \(1{\rm{ }}{{\rm{m}}^2}\) thu được số kilôgram thóc là: \(12:15 = 0,8{\rm{ }}\left( {{\rm{kg}}} \right)\).
Vậy cả thửa ruộng thu hoạch được số kilôgram thóc là: \(6{\rm{ }}000.0,8 = 4{\rm{ }}800{\rm{ }}\left( {{\rm{kg}}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đb) Sc) Đ d) Đ
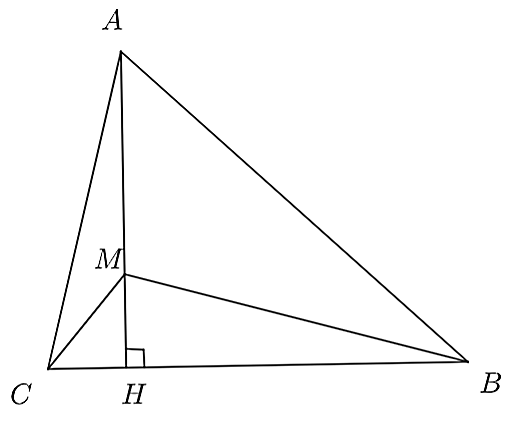
Do \(AB > AC\) (giả thiết)
Suy ra \(BH > HC\) (đường xiên lớn hơn thì hình chiếu lớn hơn)
Xét hai đường xiên \(MB\) và \(MC\) có \(BH > HC\) (cmt)
Do đó, \(MB > MC\) (hình chiếu lớn hơn thì đường xiên lớn hơn)
Ta có: \(BH\) là đường vuông góc với đường thẳng \(AH\).
Lại theo giả thiết điểm \(M\) nằm giữa hai điểm \(A\) và \(H\).
Nên \(MH < AH.\)
Suy ra \(BM < BA\) (hình chiếu lớn hơn thì đường xiên lớn hơn).
Do đó, \(BA > BM.\)
Lời giải
Hướng dẫn giải
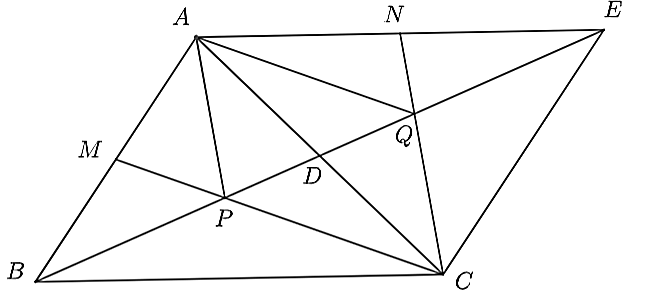
a) Gọi \(M,N\) lần lượt là trung điểm của \(AB,AE\).
Ta có: \(BP = PQ = QE\) và \(BD = DE\).
Mà \(BD = BP + PD;DE = QE + DQ\).
Suy ra \(PD = DQ\).
Hay \(D\) là trung điểm của \(PQ\).
Ta có: \(PD = \frac{1}{2}PQ\) hay \(PD = \frac{1}{2}BP\). Suy ra \(PD = \frac{1}{3}BD\)
Lại có \(BD\) là trung tuyến của \(\Delta ABC\).
Suy ra \(P\)là trọng tâm của \(\Delta ABC\).
Do đó, \(CP\) cắt \(AB\) tại trung điểm \(M.\)
Tương tự ta có: \(QD = \frac{1}{2}PQ = \frac{1}{2}QE\) hay \(QD = \frac{1}{3}ED\).
Do đó, \(Q\) là trọng tâm của tam giác \(AEC\).
Suy ra \(CQ\) cắt \(AE\) tại trung điểm \(N\).
b) Xét \(\Delta ADP\) và \(\Delta CDQ\) có:
\(AD = DC\) (gt)
\(\widehat {ADP} = \widehat {CDQ}\) (đối đỉnh)
\(PD = DQ\) (cmt)
Suy ra \(\Delta ADP = \Delta CDQ\) (c.g.c)
Suy ra \(\widehat {DAP} = \widehat {DCQ}\) (hai góc tương ứng).
Mà hai góc ở vị trí so le trong nên \(CQ\parallel AP.\)
Xét \(\Delta ADQ\) và \(\Delta CDP\) có:
\(AD = DC\) (gt)
\(\widehat {ADQ} = \widehat {CDP}\) (đối đỉnh)
\(PD = DQ\) (cmt)
Suy ra \(\Delta ADQ = \Delta CDP\) (c.g.c)
Suy ra \(\widehat {DAQ} = \widehat {DCP}\) (hai góc tương ứng).
Mà hai góc ở vị trí so le trong nên \(CP\parallel AQ\).
Câu 3
A. \(OA = \frac{2}{3}AM.\)
B. \(OM = \frac{1}{3}AM.\)
C. \(AO = \frac{2}{3}BN.\)
D. \(ON = \frac{1}{3}BN.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{1}{3}\) và \(\frac{2}{6}.\)
B. \(\frac{1}{3}\) và \(\frac{4}{5}\).
C. \(\frac{2}{6}\) và \(\frac{4}{5}\).
D. \(\frac{2}{6}\) và \(\frac{4}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.