Một bể nước có dạng hình hộp chữ nhật với chiều dài \(2,5{\rm{ m}}\). Lúc đầu bể không có nước. Sau khi đổ vào bể \(150\) thùng nước, mỗi thùng chứa \(15\) lít nước thì mực nước của bể dâng cao \(0,5{\rm{ m}}{\rm{.}}\)
a) Tính chiều rộng của bể nước.
b) Người ta đổ thêm \(120\) thùng nước nữa thì đầy bể. Hỏi bể nước cao bao nhiêu mét?
Một bể nước có dạng hình hộp chữ nhật với chiều dài \(2,5{\rm{ m}}\). Lúc đầu bể không có nước. Sau khi đổ vào bể \(150\) thùng nước, mỗi thùng chứa \(15\) lít nước thì mực nước của bể dâng cao \(0,5{\rm{ m}}{\rm{.}}\)
a) Tính chiều rộng của bể nước.
b) Người ta đổ thêm \(120\) thùng nước nữa thì đầy bể. Hỏi bể nước cao bao nhiêu mét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Thể tích nước trong thùng khi đổ \(150\) thùng nước vào bể là: \(150.15 = 2{\rm{ }}250\) (lít)
Đổi \(2{\rm{ }}250{\rm{ }}l = 2{\rm{ }}250{\rm{ d}}{{\rm{m}}^3} = 2,25{\rm{ }}{{\rm{m}}^3}\)
Chiều rộng của bể nước là \(2,25:\left( {2,5.0,5} \right) = 1,8{\rm{ }}\left( {\rm{m}} \right)\).
b) Khi đổ thêm 120 thùng nữa thì đầy bể, tức là khi đổ tất cả \(270\) thùng thì đầy bể.
Do đó, thể tích của bể nước là: \(270.15 = 4{\rm{ }}050\) (lít) = \(4,05{\rm{ }}{{\rm{m}}^3}\).
Chiều cao của bể nước là \(4,05:\left( {2,5.1,8} \right) = 0,9{\rm{ }}\left( {\rm{m}} \right)\).
Vậy chiều cao của bể nước là \(0,9{\rm{ m}}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi tổng số gói tăm mà ba lớp đã mua là \(x\) \(\left( {x \in {\mathbb{N}^*}} \right)\).
Gọi số gói tăm dự định chia cho ba lớp 7A, 7B, 7C lúc đầu lần lượt là \(a,b,c\), ta có:
\(\frac{a}{5} = \frac{b}{6} = \frac{c}{7} = \frac{{a + b + c}}{{18}} = \frac{x}{{18}}\).
Do đó, \(a = \frac{{5x}}{{18}};{\rm{ }}b = \frac{{6x}}{{18}};{\rm{ }}c = \frac{{7x}}{{18}}\) (1)
Gọi số tăm sau khi thay đổi chia cho ba lớp 7A, 7B, 7C lần lượt là \(a',b',c'\), ta có:
\(\frac{{a'}}{4} = \frac{{b'}}{5} = \frac{{c'}}{6} = \frac{{a' + b' + c'}}{{15}} = \frac{x}{{15}}\)
Do đó, ta có: \(a' = \frac{{4x}}{{15}};{\rm{ }}b' = \frac{{5x}}{{15}};{\rm{ }}c' = \frac{{6x}}{{15}}\) (2)
So sánh (1) và (2) ta nhận thấy \(a > a';{\rm{ }}b = b';{\rm{ }}c < c'\), do đó lớp 7C nhận nhiều hơn so với ban đầu.
Ta có: \(c' - c = 4\) hay \(\frac{{6x}}{{15}} - \frac{{7x}}{{18}} = 4\) hay \(\frac{x}{{90}} = 4\) nên \(x = 360\) (thỏa mãn)
Vậy số gói tăm của ba lớp đã mua là \(360\) gói.
Lời giải
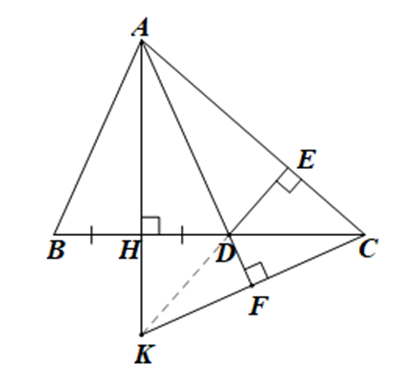
a) Xét \(\Delta ABC\) có \(AB < AC\) nên \(\widehat C < \widehat B\).
Mà \(\widehat C = 90^\circ - \widehat {HAC}\) và \(\widehat B = 90^\circ - \widehat {BAH}\).
Do đó \[90^\circ - \widehat {HAC} < 90^\circ - \widehat {BAH}\] hay \(\widehat {HAC} > \widehat {BAH}\).
b) Xét \(\Delta ABH\) và \(\Delta ADH\) có:
\(\widehat {AHB} = \widehat {AHD} = 90^\circ \);
\(AH\) là cạnh chung;
\(HB = HD\) (giả thiết).
Do đó \(\Delta ABH = \Delta ADH\) (hai cạnh góc vuông).
Suy ra \(AB = AD\) (hai cạnh tương ứng).
Tam giác \(ABD\) có \(AB = AD\) nên là tam giác cân tại \(A\).
c) Kéo dài \(AH\) và \(CF\) cắt nhau tại \(K\).
Xét \(\Delta AKC\) có \(CH \bot AK,AF \bot CK\), \(CH\) cắt \[AF\] tại \(D\) nên \(D\) là trực tâm của \(\Delta AKC\).
Suy ra \(KD \bot AC\)
Mà \(DE \bot AC\) nên ba điểm \(K,D,E\) thẳng hàng.
Vậy ba đường thẳng \(AH,DE,CF\) đồng quy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo