Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 2 = 0\) (1) với \(m\) là tham số.
a) Giải phương trình (1) khi \(m = 3.\)
b) Tìm giá trị của \(m\) để phương trình có nghiệm.
c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) sao cho:
\(A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\) đạt giá trị nhỏ nhất.
Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 2 = 0\) (1) với \(m\) là tham số.
a) Giải phương trình (1) khi \(m = 3.\)
b) Tìm giá trị của \(m\) để phương trình có nghiệm.
c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) sao cho:
\(A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\) đạt giá trị nhỏ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Với \(m = 3,\) ta có phương trình: \({x^2} - 8x + 16 = 0\) hay \({\left( {x - 4} \right)^2} = 0\), suy ra \(x - 4 = 0\).
Do đó, \(x = 4\).
Vậy phương trình có nghiệm \(x = 4\) khi \(m = 3.\)
b) Xét phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3m - 2 = 0\) có:
\(\Delta ' = {\left[ { - \left( {m + 1} \right)} \right]^2} - {m^2} - 3m + 2 = - m + 3\)
Để phương trình có nghiệm thì \(\Delta ' \ge 0\) hay \( - m + 3 \ge 0\), suy ra \(m \le 3\).
Vậy \(m \le 3\) thì phương trình có nghiệm.
c) Để phương trình (1) có hai nghiệm phân biệt thì \(\Delta ' > 0\) hay \( - m + 3 > 0\) suy ra \(m < 3.\)
Theo hệ thức Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\\{x_1}{x_2} = {m^2} + 3m - 2\end{array} \right.\).
Lại có, \(A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\)
\(A = 2018 + 5{x_1}{x_2} - \left( {2{x_1}{x_2} + x_1^2 + x_2^2} \right)\)
\(A = 2018 + 5{x_1}{x_2} - {\left( {{x_1} + {x_2}} \right)^2}\)
\(A = 2018 + 5\left( {{m^2} + 3m - 2} \right) - {\left[ {2\left( {m + 1} \right)} \right]^2}\)
\(A = 2018 + 5{m^2} + 15m - 10 - 4{m^2} - 8m - 4\)
\(A = {m^2} + 7m + 2004\)
\(A = {\left( {m + \frac{7}{2}} \right)^2} + \frac{{7967}}{4}\)
Ta có: \({\left( {m + \frac{7}{2}} \right)^2} \ge 0\) với mọi \(m\), do đó \({\left( {m + \frac{7}{2}} \right)^2} + \frac{{7967}}{4} \ge \frac{{7967}}{4}\) hay \(A \ge \frac{{7967}}{4}\).
Vậy GTNN của \(A = \frac{{7967}}{4}\) khi \(m = - \frac{7}{2}.\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điều kiện xác định: \(x \le - 2;{\rm{ }}2 \le x \le \frac{5}{2}.\)
Ta có: \({x^2} - 6x + 10 = 2\sqrt {5 - 2x} - 2\sqrt {{x^2} - 4} \)
\({x^2} - 6x + 10 - 2\sqrt {5 - 2x} + 2\sqrt {{x^2} - 4} = 0\)
\(5 - 2x - 2\sqrt {5 - 2x} + {x^2} - 4x + 4 + 2\sqrt {{x^2} - 4} = 0\)
\({\left( {\sqrt {5 - 2x} - 1} \right)^2} + {\left( {x - 2} \right)^2} + 2\sqrt {{x^2} - 4} = 0\)
Nhận thấy đồng thời \({\left( {\sqrt {5 - 2x} - 1} \right)^2} \ge 0\), \({\left( {x - 2} \right)^2} \ge 0\) và \(2\sqrt {{x^2} - 4} \ge 0\) với mọi \(x \le - 2;{\rm{ }}2 \le x \le \frac{5}{2}.\)
Do đó, để \({\left( {\sqrt {5 - 2x} - 1} \right)^2} + {\left( {x - 2} \right)^2} + 2\sqrt {{x^2} - 4} = 0\) thì đồng thời \({\left( {\sqrt {5 - 2x} - 1} \right)^2} = 0\), \({\left( {x - 2} \right)^2} = 0\) và \(2\sqrt {{x^2} - 4} = 0\).
Suy ra \(x = 2\) (thỏa mãn).
Vậy nghiệm của phương trình là \(x = 2\).
Lời giải
a) Thay \(x = - \sqrt 3 ,y = 1\) vào hàm số, ta được: \(\left( {m - 1} \right).{\left( {\sqrt 3 } \right)^2} = 1\) hay \(m - 1 = \frac{1}{3}\),
suy ra \(m = \frac{4}{3}\).
Vậy \(m = \frac{4}{3}\) thì được đồ thị hàm số \(\left( P \right):y = \frac{4}{3}{x^2}\) đi qua điểm \(A\left( { - \sqrt 3 ;1} \right).\)
b) Ta có bảng giá trị của hàm số \(\left( P \right):y = \frac{4}{3}{x^2}\) là
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = \frac{4}{3}{x^2}\) |
\(\frac{{16}}{3}\) |
\(\frac{4}{3}\) |
\(0\) |
\(\frac{4}{3}\) |
\(\frac{{16}}{3}\) |
Do đó, đồ thị hàm số \(\left( P \right):y = \frac{4}{3}{x^2}\) đi qua các điểm \(\left( { - 2;\frac{{16}}{3}} \right);\left( { - 1;\frac{4}{3}} \right);\left( {0;0} \right);\left( {2;\frac{{16}}{3}} \right);\)\(\left( {1;\frac{4}{3}} \right).\)
Từ đây, ta có đồ thị như sau:
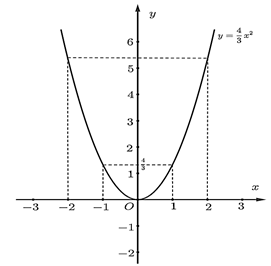
c) Thay \(x = 3\) vào hàm số \(\left( P \right):y = \frac{4}{3}{x^2}\), ta được: \(y = \frac{4}{3}{.3^2} = 12\).
Vậy điểm trên \(\left( P \right)\) có hoành độ bằng \(3\) là \(\left( {3;12} \right)\).
![1. Cho hình lục giác đều \(ABCDEG\) (các đỉnh của lục giác theo thứ tự cùng chiều kim đồng hồ) có tâm \(O.\) Phép quay ngược chiều tâm \(O\) biến điểm \(A\) thành điểm \(E\) có góc quay là bao nhiêu độ? 2. Cho đường tròn \(\left( {O;R} \right).\) Từ điểm \(M\) nằm ngoài đường tròn \[\left( {O;R} \right),\] kẻ các tiếp tuyến \[MA\] và \[MB\] với đường tròn đó \[(A,{\rm{ }}B\] là các tiếp điểm) sao cho \(MA = R\sqrt 3 .\) a) Chứng minh rằng tứ giác \(AMBO\) nội tiếp đường tròn. b) Tính bán kính đường tròn nội tiếp tam giác \(MAB.\) c) Vẽ đường thẳng \(d\) đi qua \[M\] cắt đường tròn \(\left( O \right)\) tại hai điểm \[P,{\rm{ }}Q\] sao cho \(P\) nằm giữa \(M\) và \(Q.\) Xác định vị trí của đường thẳng \[d\] sao cho \[MP + MQ\] đạt giá trị nhỏ nhất. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid13-1751337143.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập