Phương trình \[4x - 3y = 2\] nhận cặp số nào sau đây làm nghiệm?
A. \[\left( {1\,;\,\, - 2} \right)\].
B. \[\left( {1\,;\,\, - 1} \right)\].
C. \[\left( {2\,;\,\,2} \right)\].
D. \(\left( {1\,;\,\,1} \right).\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
• Thay \[x = 1\,;{\rm{ }}y = - 2\] vào phương trình đường thẳng, ta có: \(4.1 - 3.\left( { - 2} \right) = 10 \ne 2\).
Suy ra \[\left( {1\,;\,\, - 2} \right)\] không phải là nghiệm của phương trình \[4x - 3y = 2\].
• Thay \[x = 1\,;{\rm{ }}y = - 1\] vào phương trình đường thẳng, ta có: \[4.1 - 3 \cdot \left( { - 1} \right) = 7 \ne 2.\]
Suy ra \[\left( {1;\,\, - 1} \right)\] không phải là nghiệm của phương trình \[4x - 3y = 2\].
• Thay \[x = 2\,;{\rm{ }}y = 2\] vào phương trình đường thẳng, ta có: \[4.2 - 3.2 = 2\].
Suy ra \[\left( {2;\,\,2} \right)\] là nghiệm của phương trình \[4x - 3y = 2\].
• Thay \[x = 1;{\rm{ }}y = 1\] vào phương trình đường thẳng, ta có: \[4.1 - 3.1 = 1 \ne 2.\]
Suy ra \(\left( {1\,;\,\,1} \right)\) không phải là nghiệm của phương trình \[4x - 3y = 2\].
Do đó, ta chọn đáp án C.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Gọi số học sinh trường A là \(x\) (học sinh).
Gọi số học sinh trường B là \(y\) (học sinh) \(\left( {0 < x,y < 500} \right)\).
Theo đề bài, cả hai trường có tổng cộng 500 học sinh, suy ra \(x + y = 500 & \left( 1 \right)\).
Kết quả có 420 học sinh trúng tuyển trong đó có 80% học sinh trường A và \[90\% \] học sinh trường B nên ta có: \(80\% x + 90\% y = 420\) hay \(0,8x + 0,9y = 420 & \left( 2 \right)\).
Từ \(\left( 1 \right),\,\,\left( 2 \right)\) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 500\\0,8x + 0,9y = 420\end{array} \right.\).
Từ phương trình \(\left( 1 \right)\) ta có \(x + y = 500\) hay \(x = 500 - y\). Thế vào phương trình thứ (2), ta được \(0,8\left( {500 - y} \right) + 0,9y = 420\), tức là \(400 + 0,1y = 420\) suy ra \(y = 200\) (thỏa mãn).
Khi đó, \(x = 500 - 200 = 300\) (thỏa mãn).
Vậy số học sinh trường A là 300 học sinh, số học sinh trường B là 200 học sinh.
Câu 2
A. \(12,45\)cm.
B. \(15,56\,\,{\rm{cm}}{\rm{.}}\)
C. \(6,43\,\,{\rm{cm}}{\rm{.}}\)
D. \(8\)cm.
Lời giải
Đáp án đúng là: B
|
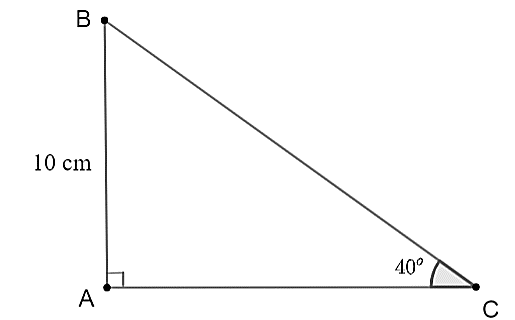
Xét tam giác \(ABC\) vuông tại \(A\) có \[\widehat C = 40^\circ \], ta có: \[AB = BC \cdot \sin {\rm{ }}C.\] Suy ra \(BC = \frac{{AB}}{{\sin C}} = \frac{{10}}{{\sin 40^\circ }} \approx 15,56\,\,\left( {{\rm{cm}}} \right).\) Vậy \[BC\] có độ dài gần nhất với đáp án B. |
|
Câu 3
A. Nếu \[a > b\] thì \(ac > bc.\)
B. Nếu \(a > b\) thì \(\frac{a}{c} > \frac{b}{c}.\)
C. Nếu \(a > b\) thì \(ac < bc.\)
D. Nếu \(a > b\) thì \(a + c < b + c.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
(2,0 điểm)
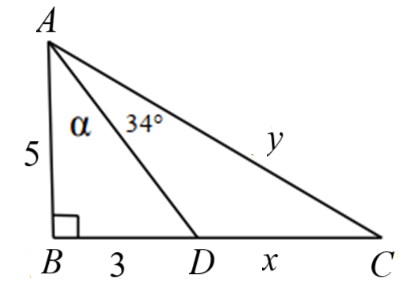
1. Cho hình vẽ bên. Tính số đo góc \(\alpha \) và các độ dài \(x,y\) (góc làm tròn đến độ, độ dài làm tròn đến hàng phần trăm).
2.
Một người đứng cách nơi thả khinh khí cầu 800 m nhìn thấy nó với góc nghiêng \(38^\circ .\) Tính độ cao của khinh khí cầu so với mặt đất. Cho biết khoảng cách từ mặt đất đến mắt người đó là \(1,5\,\,{\rm{m}}\) (kết quả làm tròn đến hàng phần mười).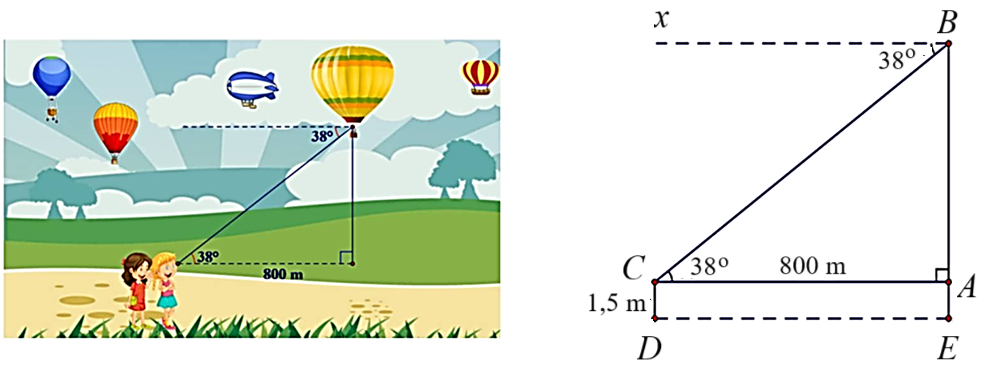
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(a < b.\)
B. \( - 3a - 3 > - 3b - 3.\)
C. \(4a < 4b.\)
D. \(3a + 1 > 3b.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(AH = 4.\)
B. \(AH = 2.\)
C. \(AH = 8.\)
D. \(AH = 3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo