Gọi \(\left( {x;\,\,y} \right)\) là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}2\left( {x + y} \right) + 3\left( {x - y} \right) = 4\\\left( {x + y} \right) + 2\left( {x - y} \right) = 5\end{array} \right..\] Bạn An sau khi giải hệ phương trình thì viết được hệ thức \(y = ax.\) Tìm \(a.\)
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp số: \(a = 13.\)
Từ phương trình \[2\left( {x + y} \right) + 3\left( {x - y} \right) = 4\] ta được \[2x + 2y + 3x - 3y = 4\] hay \[5x - y = 4.\]
Từ phương trình \[\left( {x + y} \right) + 2\left( {x - y} \right) = 5\] ta được \[x + y + 2x - 2y = 5\] hay \[3x - y = 5\].

Theo bài, \(y = ax\) nên ta có \( - \frac{{13}}{2} = a \cdot \left( { - \frac{1}{2}} \right)\), suy ra \(a = 13.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Xét tam giác \(OPQ\) vuông tại \(O\), ta có:
⦁ \(OQ = OQ \cdot \tan Q = 10 \cdot \tan 35^\circ \approx 7,00{\rm{\;(cm}});\)
⦁ \(OQ = PQ \cdot \cos Q\)
Suy ra \(PQ = \frac{{OQ}}{{\cos Q}} = \frac{{10}}{{\cos 35^\circ }} \approx 12,21{\rm{\;(cm)}}{\rm{.}}\)
Vậy \(OQ \approx 7,00{\rm{\;cm}},\,\,PQ \approx 12,21{\rm{\;cm}}.\)

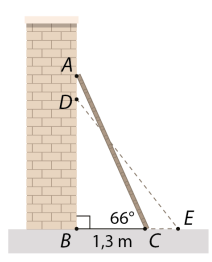
2. Xét \(\Delta ABC\) vuông tại \(A,\) ta có:
\(BC = AC \cdot \cos C\), suy ra \(AC = \frac{{BC}}{{\cos C}} = \frac{{1,3}}{{\cos 66^\circ }} \approx 3,20\) (m).
Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \(AB = BC \cdot \tan C = 1,3 \cdot \tan 66^\circ \approx 2,92\) (m).
Khi đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}} = 0,4{\rm{\;m}}\) đến vị trí \(D\) thì \(DB = AB - AD \approx 2,92 - 0,4 = 2,52\) (m) và chiều dài thang là \(DE = AC \approx 3,20\) (m).
Xét \(\Delta BDE\) vuông tại \(B,\) ta có:
\(\sin \widehat {DEB} = \frac{{BD}}{{DE}} \approx \frac{{2,52}}{{3,2}} = 0,7875\), suy ra \(\widehat {DEB} \approx 51^\circ 57'.\)
Câu 2
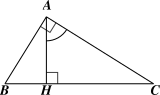
A. \(\frac{{AH}}{{AC}}\).
B. \(\frac{{AH}}{{HC}}\).
C. \(\frac{{AB}}{{BC}}\).
D. \(\frac{{AC}}{{BC}}\).
Lời giải
Đáp án đúng là: D
|
Xét \(\Delta HAC\) vuông tại \(H\) ta có: \(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\). Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin B = \frac{{AC}}{{BC}}\). Mà \(\widehat {HAC} + \widehat {C\,} = 90^\circ \) và \(\widehat {B\,} + \widehat {C\,} = 90^\circ \) nên \(\sin \widehat {HAC} = \sin B = \frac{{AC}}{{BC}}\) |
|
Vậy ta chọn phương án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( {x;\,\,2} \right)\) với \(x \in \mathbb{R}\).
B. \(\left( {2;\,\,y} \right)\) với \(y \in \mathbb{R}\).
C. \(\left( {x;\,\,0} \right)\) với \(x \in \mathbb{R}\).
D. \(\left( {0;\,\,y} \right)\) với \(y \in \mathbb{R}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.