(0,5 điểm) Cho góc \(\alpha \) thỏa mãn \[0^\circ < \alpha < 90^\circ .\] Chứng minh rằng: \[\frac{{\sin \alpha + \cos \alpha - 1}}{{1 - \cos \alpha }} = \frac{{2\cos \alpha }}{{\sin \alpha - \cos \alpha + 1}}.\]
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
Xét \(\Delta ABC\) vuông tại \(A\) có \(\widehat {B\,} = \alpha \). Do \(\widehat {B\,}\) là góc nhọn nên \(0^\circ < \widehat {B\,} < 90^\circ \) hay \[0^\circ < \alpha < 90^\circ .\] Ta có: \(\sin \alpha = \frac{{AC}}{{BC}}\) và \(\cos \alpha = \frac{{AB}}{{BC}}.\) \(B{C^2} = A{B^2} + A{C^2}\) (định lí Pythagore). |
|
Khi đó:
\[{\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2} = \frac{{A{C^2}}}{{B{C^2}}} + \frac{{A{B^2}}}{{B{C^2}}} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1.\]
Với \[0^\circ < \alpha < 90^\circ \] thì \[1 - \cos \alpha \ne 0\] và \[\sin \alpha - \cos \alpha + 1 \ne 0\].
Ta có: \[\frac{{\sin \alpha + \cos \alpha - 1}}{{1 - \cos \alpha }} - \frac{{2\cos \alpha }}{{\sin \alpha - \cos \alpha + 1}}\]
\[ = \frac{{\left( {\sin \alpha + \cos \alpha - 1} \right)\left( {\sin \alpha - \cos \alpha + 1} \right) - 2\cos \alpha \left( {1 - \cos \alpha } \right)}}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{\left[ {\sin \alpha + \left( {\cos \alpha - 1} \right)} \right]\left[ {\sin \alpha - \left( {\cos \alpha - 1} \right)} \right] - 2\cos \alpha \left( {1 - \cos \alpha } \right)}}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}\alpha - {{\left( {\cos \alpha - 1} \right)}^2} - 2\cos \alpha + 2{{\cos }^2}\alpha }}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}\alpha - \left( {{{\cos }^2}\alpha - 2\cos \alpha + 1} \right) - 2\cos \alpha + 2{{\cos }^2}\alpha }}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}\alpha - {{\cos }^2}\alpha + 2\cos \alpha - 1 - 2\cos \alpha + 2{{\cos }^2}\alpha }}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}x + {{\cos }^2}x - 1}}{{\left( {1 - \cos x} \right)\left( {\sin x - \cos x + 1} \right)}}.\]
\[ = \frac{{1 - 1}}{{\left( {1 - \cos x} \right)\left( {\sin x - \cos x + 1} \right)}} = 0\] (vì \[1 - \cos x \ne 0\] và \[\sin x - \cos x + 1 \ne 0)\]
Vậy \[\frac{{\sin x + \cos x - 1}}{{1 - \cos x}} = \frac{{2\cos x}}{{\sin x - \cos x + 1}}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Xét tam giác \(OPQ\) vuông tại \(O\), ta có:
⦁ \(OQ = OQ \cdot \tan Q = 10 \cdot \tan 35^\circ \approx 7,00{\rm{\;(cm}});\)
⦁ \(OQ = PQ \cdot \cos Q\)
Suy ra \(PQ = \frac{{OQ}}{{\cos Q}} = \frac{{10}}{{\cos 35^\circ }} \approx 12,21{\rm{\;(cm)}}{\rm{.}}\)
Vậy \(OQ \approx 7,00{\rm{\;cm}},\,\,PQ \approx 12,21{\rm{\;cm}}.\)
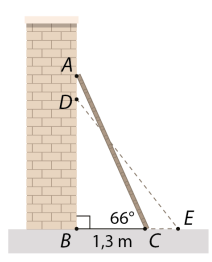
2. Xét \(\Delta ABC\) vuông tại \(A,\) ta có:
\(BC = AC \cdot \cos C\), suy ra \(AC = \frac{{BC}}{{\cos C}} = \frac{{1,3}}{{\cos 66^\circ }} \approx 3,20\) (m).
Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \(AB = BC \cdot \tan C = 1,3 \cdot \tan 66^\circ \approx 2,92\) (m).
Khi đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}} = 0,4{\rm{\;m}}\) đến vị trí \(D\) thì \(DB = AB - AD \approx 2,92 - 0,4 = 2,52\) (m) và chiều dài thang là \(DE = AC \approx 3,20\) (m).
Xét \(\Delta BDE\) vuông tại \(B,\) ta có:
\(\sin \widehat {DEB} = \frac{{BD}}{{DE}} \approx \frac{{2,52}}{{3,2}} = 0,7875\), suy ra \(\widehat {DEB} \approx 51^\circ 57'.\)
Câu 2
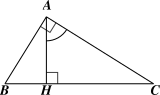
A. \(\frac{{AH}}{{AC}}\).
B. \(\frac{{AH}}{{HC}}\).
C. \(\frac{{AB}}{{BC}}\).
D. \(\frac{{AC}}{{BC}}\).
Lời giải
Đáp án đúng là: D
|
Xét \(\Delta HAC\) vuông tại \(H\) ta có: \(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\). Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin B = \frac{{AC}}{{BC}}\). Mà \(\widehat {HAC} + \widehat {C\,} = 90^\circ \) và \(\widehat {B\,} + \widehat {C\,} = 90^\circ \) nên \(\sin \widehat {HAC} = \sin B = \frac{{AC}}{{BC}}\) |
|
Vậy ta chọn phương án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( {x;\,\,2} \right)\) với \(x \in \mathbb{R}\).
B. \(\left( {2;\,\,y} \right)\) với \(y \in \mathbb{R}\).
C. \(\left( {x;\,\,0} \right)\) với \(x \in \mathbb{R}\).
D. \(\left( {0;\,\,y} \right)\) với \(y \in \mathbb{R}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập