Giá trị \(\sin 27^\circ \) (kết quả làm tròn đến chữ số thập phân thứ ba) bằng
A. \(0,450\).
B. \(0,453\).
C. \(0,454\).
D. \(0,455\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: C
Sử dụng máy tính cầm tay ta lần lượt bấm các phím
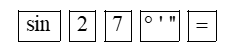
Trên màn hình hiện kết quả \(0,4539904997\), làm tròn kết quả đến chữ số thập phân thứ ba, ta được \(0,454\). Như vậy \(\sin 27^\circ \approx 0,454\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(b = a \cdot \sin B = a \cdot \cos C\).
B. \(a = c \cdot \tan B = c \cdot \cot C\).
C. \({a^2} = {b^2} + {c^2}.\)
D. \(c = a \cdot \sin C = a \cdot \cos B\).
Lời giải
Đáp án đúng là: B
|
Xét \(\Delta ABC\) vuông tại \(A,\) ta có: ⦁ \[B{C^2} = A{C^2} + A{B^2}\] hay \({a^2} = {b^2} + {c^2}\) (định lí Pythagore); ⦁ \[AC = BC \cdot \sin B = BC \cdot \cos C\] hay \(b = a \cdot \sin B = a \cdot \cos C\); ⦁ \(AB = BC \cdot \sin C = BC \cdot \cos B\) hay \(c = a \cdot \sin C = a \cdot \cos B\); Như vậy các khẳng định A, C, D đều đúng. Ta chọn phương án B. |
|
Câu 2
A. \(\left( {x - 1} \right)\left( {x + 1} \right) = 0\).
B. \(x\left( {x + 1} \right) = 0\).
C. \(x = 0\).
D. \(x\left( {x - 1} \right) = 0\).
Lời giải
Đáp án đúng là: B
Dễ dàng thấy rằng:
⦁ Giá trị \(x = 0\) không là nghiệm của phương trình \(\left( {x - 1} \right)\left( {x + 1} \right) = 0\).
⦁ Giá trị \(x = 0\) và \(x = - 1\) là nghiệm của phương trình \(x\left( {x + 1} \right) = 0\).
⦁ Giá trị \(x = - 1\) không là nghiệm của phương trình \(x = 0\) và phương trình \(x\left( {x - 1} \right) = 0\)
Vậy ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
