Mô hình toán học sau đây được sử dụng trong quan sát chuyển động của một vật. Trong không gian cho hệ trục tọa độ Oxyz có 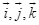 lần lượt là các vectơ đơn vị trên các trục
lần lượt là các vectơ đơn vị trên các trục  và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm
và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm 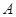 và
và 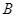 , trong đó điểm
, trong đó điểm 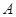 có tọa độ là
có tọa độ là 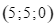 . Một vật (coi như một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian t (giây) theo công thức
. Một vật (coi như một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian t (giây) theo công thức 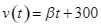 (m/giây), trong đó
(m/giây), trong đó 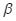 là hằng số dương và
là hằng số dương và 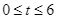 . Ở thời điểm ban đầu
. Ở thời điểm ban đầu 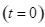 , vật đi qua A với tốc độ 300 m/giây và hướng tới
, vật đi qua A với tốc độ 300 m/giây và hướng tới 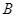 . Sau
. Sau 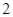 giây kể từ thời điểm ban đầu, vật đi được quãng đường
giây kể từ thời điểm ban đầu, vật đi được quãng đường 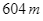 . Gọi
. Gọi 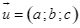 là vectơ cùng hướng với vectơ
là vectơ cùng hướng với vectơ 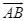 . Biết rằng
. Biết rằng 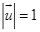 và góc giữa vectơ
và góc giữa vectơ 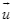 lần lượt với các vectơ
lần lượt với các vectơ 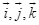 có số đo tương ứng bằng
có số đo tương ứng bằng 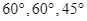 .
.
a) 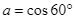 .
.
b) Phương trình đường thẳng 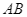 là
là 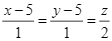 .
.
c) 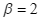 .
.
d) Giả sử sau 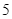 giây kể từ thời điểm ban đầu, vật đến điểm
giây kể từ thời điểm ban đầu, vật đến điểm 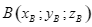 . Khi đó
. Khi đó 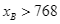 .
.
Mô hình toán học sau đây được sử dụng trong quan sát chuyển động của một vật. Trong không gian cho hệ trục tọa độ Oxyz có ![]() lần lượt là các vectơ đơn vị trên các trục
lần lượt là các vectơ đơn vị trên các trục ![]() và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm
và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm ![]() và
và ![]() , trong đó điểm
, trong đó điểm ![]() có tọa độ là
có tọa độ là ![]() . Một vật (coi như một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian t (giây) theo công thức
. Một vật (coi như một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian t (giây) theo công thức ![]() (m/giây), trong đó
(m/giây), trong đó ![]() là hằng số dương và
là hằng số dương và ![]() . Ở thời điểm ban đầu
. Ở thời điểm ban đầu ![]() , vật đi qua A với tốc độ 300 m/giây và hướng tới
, vật đi qua A với tốc độ 300 m/giây và hướng tới ![]() . Sau
. Sau ![]() giây kể từ thời điểm ban đầu, vật đi được quãng đường
giây kể từ thời điểm ban đầu, vật đi được quãng đường ![]() . Gọi
. Gọi ![]() là vectơ cùng hướng với vectơ
là vectơ cùng hướng với vectơ ![]() . Biết rằng
. Biết rằng ![]() và góc giữa vectơ
và góc giữa vectơ ![]() lần lượt với các vectơ
lần lượt với các vectơ ![]() có số đo tương ứng bằng
có số đo tương ứng bằng ![]() .
.
a) ![]() .
.
b) Phương trình đường thẳng ![]() là
là ![]() .
.
c) ![]() .
.
d) Giả sử sau ![]() giây kể từ thời điểm ban đầu, vật đến điểm
giây kể từ thời điểm ban đầu, vật đến điểm ![]() . Khi đó
. Khi đó ![]() .
.
Quảng cáo
Trả lời:
Chọn a) Đúng | b) Sai | c) Đúng | d) Sai
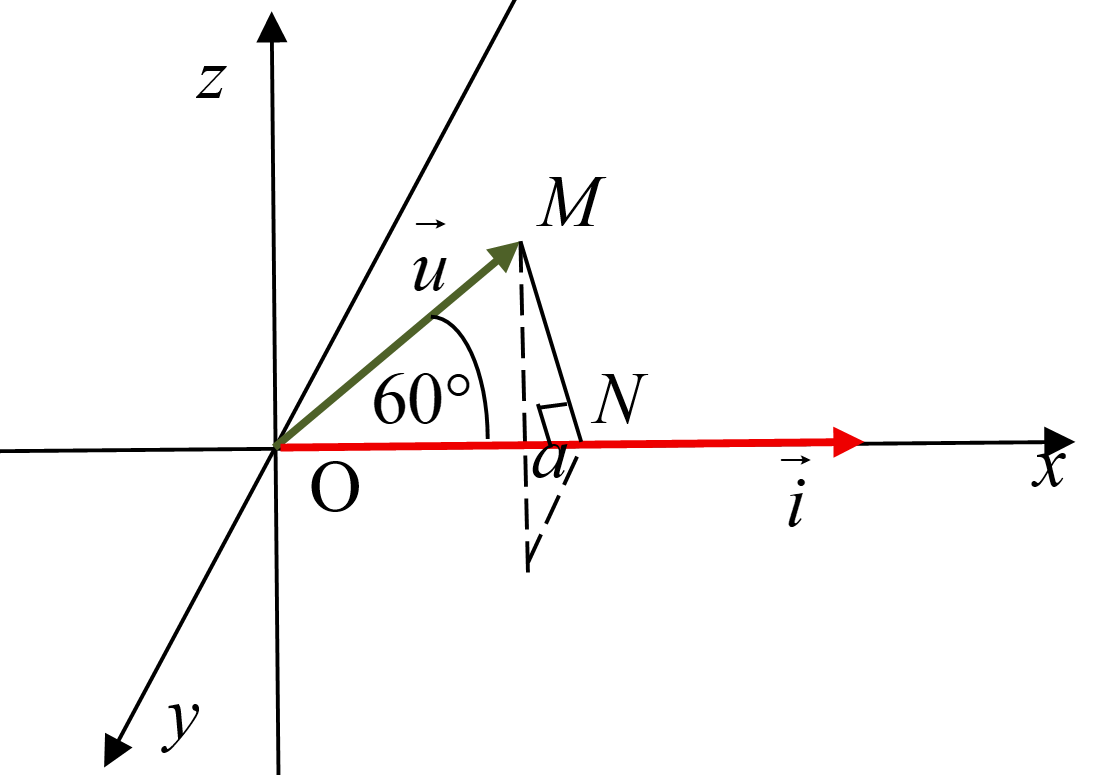
a) Vì góc giữa vectơ ![]() với vectơ
với vectơ ![]() là
là ![]() . Nên ta có:
. Nên ta có:
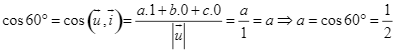 .
.
Chọn ĐÚNG.
b) Ta có:
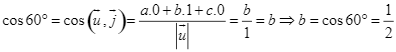 ;
;
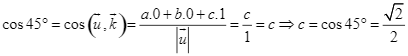 ;
;
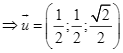 .
.
Theo giả thiết ![]() là vectơ cùng hướng với vectơ
là vectơ cùng hướng với vectơ ![]() nên
nên ![]() là VTCP của
là VTCP của![]() .
.
Vậy đường thẳng ![]() có:
có: ![]() và có 1 VTCP
và có 1 VTCP ![]() .
.
Nên phương trình chính tắc của đường thẳng ![]() là:
là: ![]() .
.
Chọn SAI.
c) Ở thời điểm ban đầu ![]() , vật đi qua
, vật đi qua ![]() và hướng tới
và hướng tới ![]() . Sau
. Sau ![]() giây kể từ thời điểm ban đầu, vật đi được quãng đường
giây kể từ thời điểm ban đầu, vật đi được quãng đường![]() . Ta có:
. Ta có:
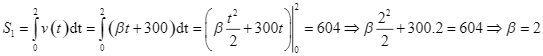 .
.
Chọn ĐÚNG.
d) Sau ![]() giây kể từ thời điểm ban đầu, vật đến điểm
giây kể từ thời điểm ban đầu, vật đến điểm ![]() . Ta có:
. Ta có:
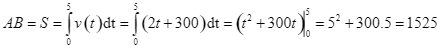 .
.
Theo giả thiết ![]() là vectơ cùng hướng với vectơ
là vectơ cùng hướng với vectơ ![]() nên:
nên:
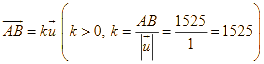
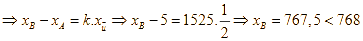
.
Chọn SAI.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 1260
Bộ ba số xuất hiện ở những bộ ba vị trí ![]()
![]()
![]() tạo thành các cấp số cộng theo thứ tự đó thì
tạo thành các cấp số cộng theo thứ tự đó thì 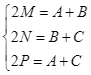 . Khi đó:
. Khi đó: ![]() phải cùng chẵn hoặc cùng lẻ.
phải cùng chẵn hoặc cùng lẻ.
Các trường hợp không hợp lệ: Nếu ![]() là một cấp số cộng (giả sử
là một cấp số cộng (giả sử ![]() ),
), ![]() ,
, ![]() ) thì
) thì ![]() phải là số chẵn để
phải là số chẵn để ![]() cùng tính chẵn lẻ. Khi đó
cùng tính chẵn lẻ. Khi đó ![]() ,
, ![]() ,
, ![]() . Giá trị
. Giá trị ![]() trùng với
trùng với ![]() . Vì 6 số được xếp phải đôi một khác nhau nên mọi bộ
. Vì 6 số được xếp phải đôi một khác nhau nên mọi bộ ![]() là cấp số cộng sẽ không hợp lệ.
là cấp số cộng sẽ không hợp lệ.
Số cách chọn 6 số từ 9 số và xếp là: ![]() .
.
Trường hợp 1: ![]() đều chẵn
đều chẵn
Số cách chọn 3 số chẵn: ![]() .
.
Các bộ ![]() số chẵn là cấp số cộng:
số chẵn là cấp số cộng: ![]() và
và ![]() , hai bộ này không hợp lệ.
, hai bộ này không hợp lệ.
Số bộ 3 số chẵn hợp lệ: ![]() .
.
Số trường hợp thuận lợi khi ![]() đều chẵn:
đều chẵn: ![]() .
.
Trường hợp 2: ![]() đều lẻ
đều lẻ
Số cách chọn 3 số lẻ: ![]() .
.
Các bộ ![]() số lẻ là cấp số cộng có:
số lẻ là cấp số cộng có: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , bốn bộ này không hợp lệ.
, bốn bộ này không hợp lệ.
Số bộ 3 số lẻ hợp lệ: ![]() .
.
Số trường hợp thuận lợi khi ![]() đều lẻ:
đều lẻ: ![]()
Cả hai trường hợp có số kết quả thuận lợi là: ![]() .
.
Xác suất cần tìm: 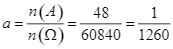
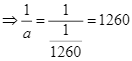 .
.
Lời giải
Chọn a) Đúng | b) Đúng| c) Sai | d) Đúng
Gọi các biến cố:
![]() : “Tin nhắn bị đánh dấu”;
: “Tin nhắn bị đánh dấu”; ![]() : “Tin nhắn là quảng cáo”.
: “Tin nhắn là quảng cáo”.
Theo đề cho: ![]() .
.
Chọn ngẫu nhiên một tin nhắn được gửi đến điện thoại.
a) Xác suất để tin nhắn đó không bị đánh dấu là:
![]()
Chọn ĐÚNG.
b) Xác suất để tin nhắn đó không phải là quảng cáo, biết rằng nó không bị đánh dấu là:
![]()
Chọn ĐÚNG.
c) Xác suất để tin nhắn đó không phải là quảng cáo là:
![]()
Chọn SAI.
d) Xác suất để tin nhắn đó không bị đánh dấu, biết rằng nó không phải là quảng cáo là:
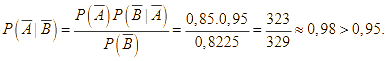
Chọn ĐÚNG.
(*) Cách 2: đề xuất bởi GV Tu Duy
Lập bảng thống kê 2x2:
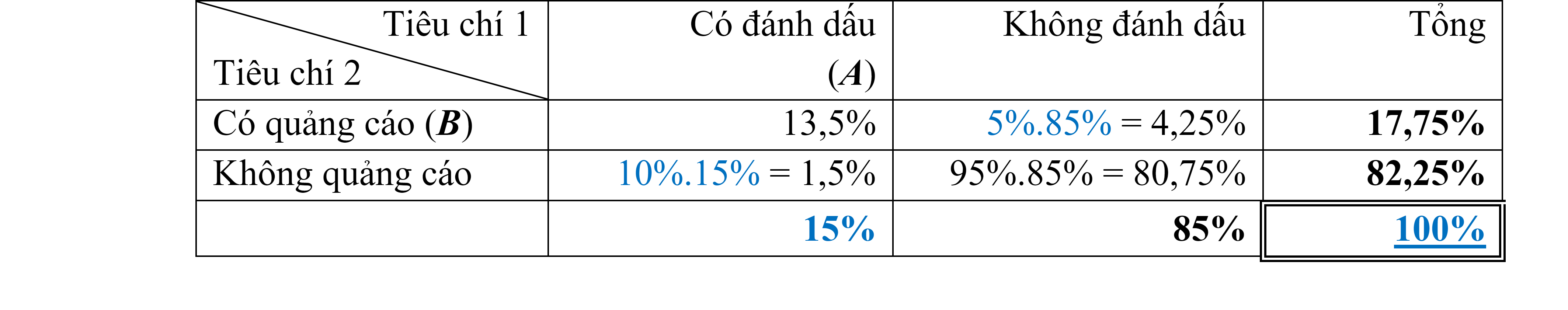
a) Xác suất để tin nhắn không bị đánh dấu: ![]() .
.
b) Xác suất để tin nhắn không phải là quảng cáo, biết rằng nó không bị đánh dấu:
![]() .
.
c) Xác suất để tin nhắn không phải quảng cáo: ![]() .
.
d) Xác suất để tin nhắn không bị đánh dấu, biết rằng nó không phải là quảng cáo:
![]() .
.
Câu 3
Nếu một doanh nghiệp sản xuất 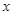 sản phẩm trong một tháng (
sản phẩm trong một tháng (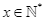 ;
; 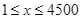 ) thì doanh thu nhận được khi bán hết số sản phẩm đó là
) thì doanh thu nhận được khi bán hết số sản phẩm đó là 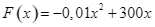 (nghìn đồng), trong khi chi phí sản xuất bình quân cho mỗi sản phẩm là
(nghìn đồng), trong khi chi phí sản xuất bình quân cho mỗi sản phẩm là 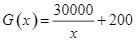 (nghìn đồng). Giả sử số sản phẩm sản xuất ra luôn được bán hết. Trong một tháng, doanh nghiệp đó cần sản xuất ít nhất bao nhiêu sản phẩm để lợi nhuận thu được lớn hơn
(nghìn đồng). Giả sử số sản phẩm sản xuất ra luôn được bán hết. Trong một tháng, doanh nghiệp đó cần sản xuất ít nhất bao nhiêu sản phẩm để lợi nhuận thu được lớn hơn 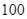 triệu đồng?
triệu đồng?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.