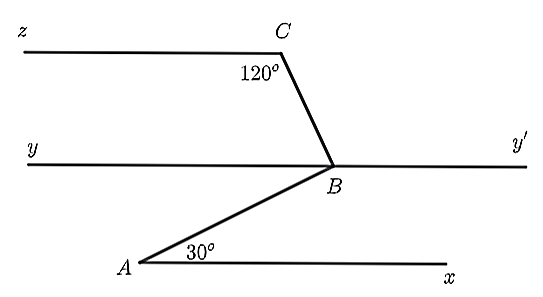
Cho hình vẽ. Biết \(\widehat B = 65^\circ ,\)\(\widehat {ACB} = 50^\circ \), hai tia \(Cx\) và \(CB\) đối nhau, tia \(Cy\) là tia phân giác của \(\widehat {ACx}\).
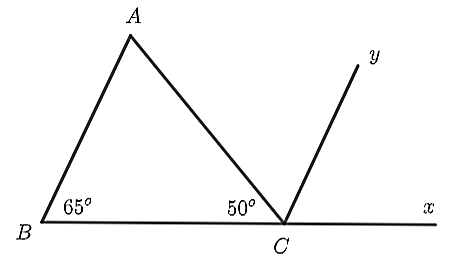
Hỏi số đo \(\widehat {ACy}\) bằng bao nhiêu độ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: \(65\)
Vì hai tia \(Cx\) và \(CB\) đối nhau nên \(\widehat {xCB}\) là góc bẹt.
Ta có \(\widehat {ACB}\) và \(\widehat {ACx}\) là hai góc kề bù nên \(\widehat {ACB} + \widehat {ACx} = 180^\circ \) hay \(50^\circ + \widehat {ACx} = 180^\circ \)
Suy ra \(\widehat {ACx} = 180^\circ - 50^\circ = 130^\circ \).
Lại có tia \(Cy\) là tia phân giác của \(\widehat {ACx}\) nên \(\widehat {ACy} = \widehat {yCx} = \widehat {\frac{{ACx}}{2}} = 65^\circ \).
Vậy \(\widehat {ACy} = 65^\circ \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) Vì \(Ax\parallel yy'\) nên \(\widehat {xAB} = \widehat {ABy} = 30^\circ \) (so le trong).
b) Ta có \(Ax\parallel Cz\) mà \(Ax\parallel yy'\) nên \(yy'\parallel Cz\).
Vì \(Ax\parallel yy'\) nên \(\widehat {BAx} = \widehat {ABy} = 30^\circ \)(so le trong)
Vì \(yy'\parallel Cz\) nên \(\widehat {zCB} = \widehat {CBy'} = 120^\circ \) (so le trong)
Ta có: \(\widehat {CBy'}\) và \(\widehat {CBy}\) là hai góc kề bù nên \(\widehat {CBy'} + \widehat {CBy} = 180^\circ \).
hay \(\widehat {CBy} = 180^\circ - \widehat {CBy'} = 180^\circ - 120^\circ = 60^\circ .\)
Lại có \(\widehat {CBy}\) và \(\widehat {ABy}\) là hai góc kề nhau nên \(\widehat {CBy} + \widehat {ABy} = \widehat {ABC}\).
Do đó, \(\widehat {ABC} = 30^\circ + 60^\circ = 90^\circ \).
c)
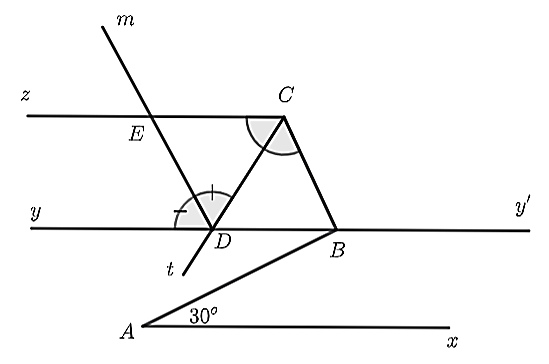
Vì tia \(Ct\) là tia phân giác của \(\widehat {BCz}\) nên \(\widehat {BCD} = \widehat {DCE} = \widehat {\frac{{BCz}}{2}} = \frac{{120^\circ }}{2} = 60^\circ \).
Do \(yy'\parallel Cz\) nên \(\widehat {DCE} = \widehat {CDB} = 60^\circ \) (so le trong)
Mà \(\widehat {CDB}\) và \(\widehat {CDy}\) là hai góc kề bù nên \(\widehat {CDy} + \widehat {CDB} = 180^\circ \) hay \(\widehat {CDy} + 60^\circ = 180^\circ \).
Suy ra \(\widehat {CDy} = 180^\circ - \widehat {CDB} = 180^\circ - 60^\circ = 120^\circ \).
Vì tia \(Dm\) là tia phân giác \(\widehat {CDy}\) nên \(\widehat {EDC} = \widehat {\frac{{CDy}}{2}} = \frac{{120^\circ }}{2} = 60^\circ .\)
Vậy \(\widehat {EDC} = 60^\circ .\)
Lời giải
Hướng dẫn giải
Đáp án: \(1,5\)
Diện tích kính cường lực dùng để làm vỏ chính là diện tích xung quanh của máy lọc nước.
Do đó, diện tích kính cường lực cần dùng để làm vỏ là: \(2.\left( {35 + 44} \right).95 = 15010\) (cm2).
Đổi \(15010{\rm{ c}}{{\rm{m}}^2} = 1,5010{\rm{ }}{{\rm{m}}^2}\).
Làm tròn \(1,5010{\rm{ }}{{\rm{m}}^2}\) đến hàng phần mười ta được \(1,5{\rm{ }}{{\rm{m}}^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{ - 75}}{{1000}}.\)
B. \(\frac{{ - 3}}{4}.\)
C. \(\frac{{ - 75}}{{100}}.\)
D. \(\frac{{ - 75}}{{10}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập