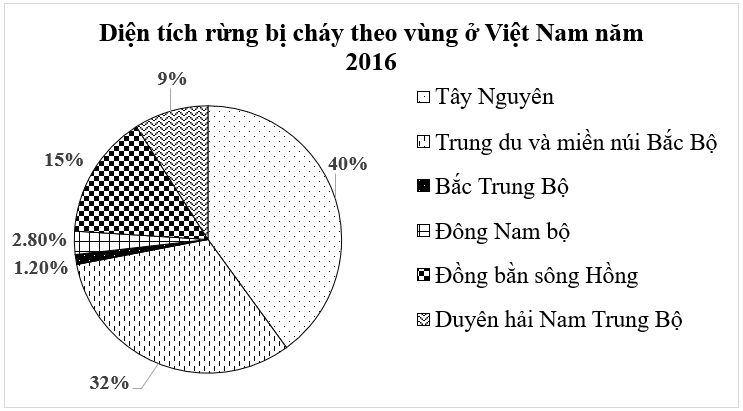
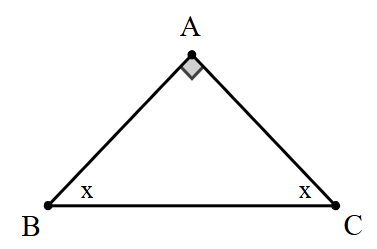
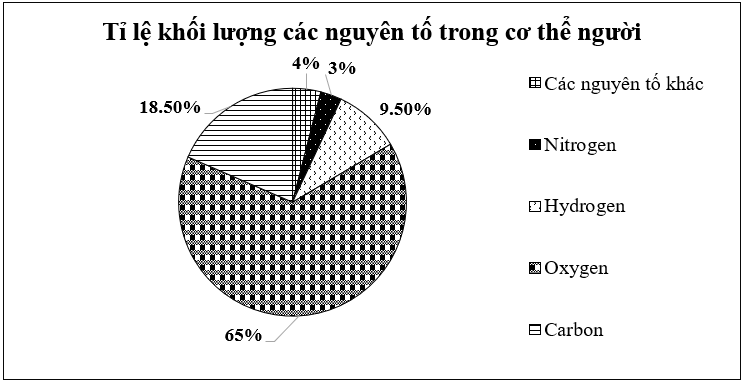
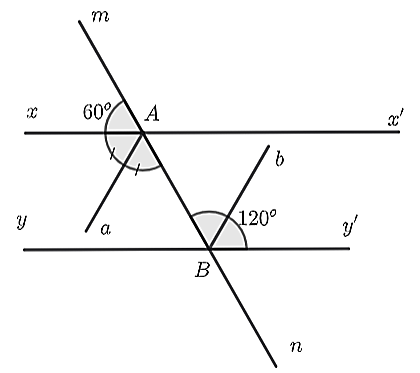
Cho biểu đồ sau:

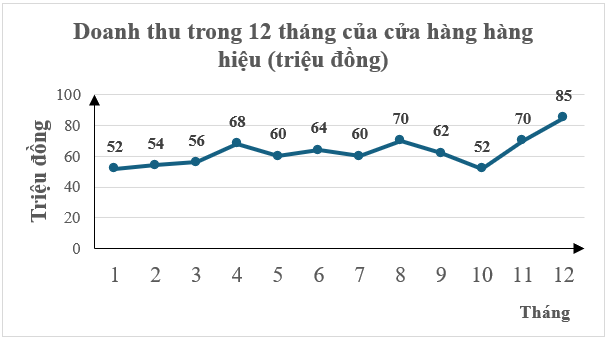
Tháng nào cửa hàng có doanh thu cao nhất?

Hướng dẫn giải

Nhận thấy \(\left| {x + \frac{1}{{101}}} \right| \ge 0;\) \(\left| {x + \frac{2}{{101}}} \right| \ge 0;\) \(\left| {x + \frac{3}{{101}}} \right| \ge 0\)…..;\(\left| {x + \frac{{100}}{{101}}} \right| \ge 0\)

Do đó, \(\left| {x + \frac{1}{{101}}} \right| + \left| {x + \frac{2}{{101}}} \right| + \left| {x + \frac{3}{{101}}} \right| + ... + \left| {x + \frac{{100}}{{101}}} \right| \ge 0\).

Mà \(\left| {x + \frac{1}{{101}}} \right| + \left| {x + \frac{2}{{101}}} \right| + \left| {x + \frac{3}{{101}}} \right| + ... + \left| {x + \frac{{100}}{{101}}} \right| = 101x\) nên \(101x \ge 0\) hay \(x \ge 0\).

Với \(x \ge 0\), suy ra \(x + \frac{1}{{101}} + x + \frac{2}{{101}} + x + \frac{3}{{101}} + ... + x + \frac{{100}}{{101}} = 101x\)

\(100x + \left( {\frac{1}{{101}} + \frac{2}{{101}} + \frac{3}{{101}} + ... + \frac{{100}}{{101}}} \right) = 101x\)

\(101x - 100x = \frac{{1 + 2 + 3 + ... + 100}}{{101}}\)

\(x = \frac{{100.101}}{{2.101}}\)

\(x = 50\) (thỏa mãn)

Vậy \(x = 50\).

Hướng dẫn giải

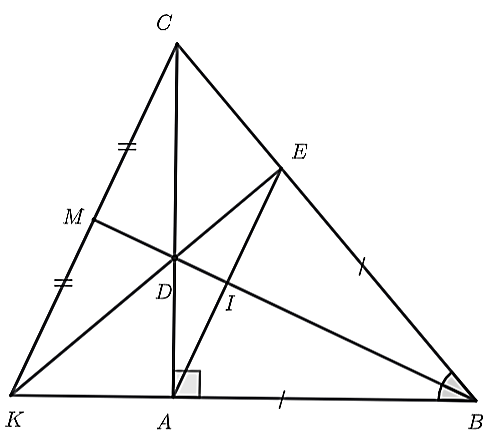
a) Xét \(\Delta ABD\) và \(\Delta EBD\), có:

\(AB = EB\) (gt)

\(\widehat {ABD} = \widehat {DBE}\) (\(BD\) là phân giác của \(\widehat {ABC}\))

\(BD\) chung

Do đó, \(\Delta ABD = \Delta EBD\) (c.g.c)

b) Xét \(\Delta ABI\) và \(\Delta EBI,\) có:

\(AB = BE\) (gt)

\(\widehat {ABI} = \widehat {IBE}\) (\(BD\) là phân giác của \(\widehat {ABC}\))

\(BI\) chung

Do đó, \(\Delta ABI = \Delta EBI\) (c.g.c)

Suy ra \(AI = IE\) (hai cạnh tương ứng)

Mà \(I\) là giao điểm của \(BD\) và \(AE.\)

Do đó, \(I\) là trung điểm của \(AE.\)

c) Vì \(\Delta ABD = \Delta EBD\) (cmt) suy ra \(AD = DE\) (hai cạnh tương ứng)

và \(\widehat {DAB} = \widehat {DEB} = 90^\circ \) (hai góc tương ứng).

Nhận thấy, \(\Delta ADK\) vuông tại \(A\) và \(\Delta EDC\) vuông tại \(E\) có:

\(AD = DE\) (cmt)

\(\widehat {ADK} = \widehat {EDC}\) (đối đỉnh)

Suy ra \(\Delta ADK = \Delta EDC\) (cgv – gn)

Do đó, \(CE = AK\) (hai cạnh tương ứng)

Ta có: \(KB = KA + AB\); \(CB = CE + EB\)

Mà \(AB = BE\) (gt); \(AK = CE\) (cmt)

Do đó, \(KB = CB\).

Xét \(\Delta KMB\) và \(\Delta CMB\) có:

\(KB = CB\) (cmt)

\(KM = CM\) (gt)

\(MB\) chung

Do đó, \(\Delta KMB = \Delta CMB\) (c.c.c)

Suy ra \(\widehat {CBM} = \widehat {KBM}\) (hai góc tương ứng)

Mà tia \(BM\) nằm giữa hai tia \(BK,BC\) nên \(BM\) là tia phân giác của \(\widehat {KBC}\).

Mặt khác, \(BD\) cũng là tia phân giác của \(\widehat {ABC}\).

Do đó, ba điểm \(B,D,M\) thẳng hàng.