(1,5 điểm) Cho \(\Delta ABC\) có \(AB = AC.\) Gọi \(K\) là trung điểm của đoạn thẳng \(BC.\) Trên tia đối của tia \(KA,\) lấy điểm \(H\) sao cho \(KH = KA\).

a) Chứng minh rằng \(\Delta AKC = \Delta AKB.\)

b) Chứng minh \(AC\parallel HB.\)

c) Từ \(K\) kẻ \(KM \bot AC\) \(\left( {M \in AC} \right)\); \(KN \bot BH\) \(\left( {N \in BH} \right)\). Chứng minh rằng ba điểm \(M,K,N\) thẳng hàng.

Hướng dẫn giải

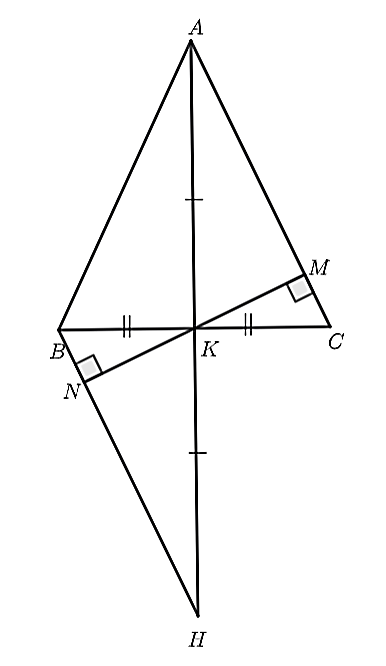
a) Xét \(\Delta AKC\) và \(\Delta AKB,\) có:

\(AB = AC\) (gt)

\(BK = KC\)(gt)

\(AK\) chung

Do đó, \(\Delta AKC = \Delta AKB\) (c.c.c)

b) Vì \(\Delta AKC = \Delta AKB\) (cmt) nên \(\widehat {ABK} = \widehat {ACK}\) (hai góc tương ứng) và \(\widehat {AKB} = \widehat {AKC} = 90^\circ \) (hai góc tương ứng)

Xét \(\Delta AKB\) và \(\Delta HKB\), có:

\(BK\) chung

\(AH = HK\)

\(\widehat {AKB} = \widehat {BKH} = 90^\circ \)

Do đó, \(\Delta AKB = \Delta HKB\) (c.g.c)

Suy ra \(\widehat {ABK} = \widehat {HBK}\) (hai cạnh tương ứng).

Mà \(\widehat {ABK} = \widehat {ACK}\) nên \(\widehat {HBK} = \widehat {ACK}\).

Mà hai góc ở vị trí so le trong nên \(BH\parallel AC\).

c) Xét \(\Delta NKH\) và \(\Delta MKA\), có:

\(AK = KH\) (gt)

\(\widehat {KNH} = \widehat {KMA} = 90^\circ \)

\(\widehat {NHK} = \widehat {KAM}\) (so le trong)

Do đó, \(\Delta NKH = \Delta MKA\) (cgv – gn)

Suy ra \(\widehat {NKH} = \widehat {AKM}\) (hai góc tương ứng)

Lại có, \(\widehat {NKH} + \widehat {NKA} = 180^\circ \) (hai góc kề bù) nên \(\widehat {NKA} + \widehat {AKM} = 180^\circ \) hay \(\widehat {NKM} = 180^\circ \).

Vậy ba điểm \(N,K,M\) thẳng hàng.