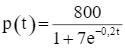Tìm tất cả các số nguyên k để phương trình kx2 – (1 – 2k)x + k – 2 = 0 luôn luôn có nghiệm số hữu tỉ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: kx2 – (1 – 2k)x + k – 2 = 0 (*)
(*) với k = 0
Phương trình (*) ⇔ x − 2 = 0
⇔ x = 2
(*) với k khác 0 thì phương trình (*) là phương trình bậc 2
Δ = (1 − 2k)2 − 4k(k − 2) = 4k2 − 4k + 1 – 4k2 + 8k = 4k + 1
Để pt có nghiệm hữu tỉ khi 4k + 1 là số chính phương
⇒ 4k+1= a2 (1)
Vì 4k + 1 là số lẻ ⇒ a2 là số lẻ
⇒ a là số lẻ
⇒ a = 2n + 1 (n thuộc Z) thay vào (1) ta có
4k + 1 = (2n + 1)2 = 4n2 + 4n + 1
⇔ 4k = 4n(n + 1)
⇔ k = n(n + 1)
Vậy với k = n(n + 1) thì phương trình luôn có nghiệm hữu tỉ (n thuộc Z).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
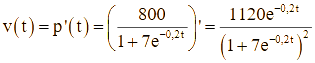
Bấm máy khảo sát v(t) ta được v(t) lớn nhất tại t ≈ 9,73.
Lời giải
Gọi x (m) là chiều dài, y (m) là chiều rộng của thửa ruộng hình chữ nhật
Thửa ruộng hình chữ nhật có chu vi 250m
⇒ (x + y) . 2 = 250
⇔ x + y = 125 (1)
Chiều dài giảm 3 lần, chiều rộng tăng 2 lần thì chu vi không đổi
⇒ 
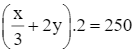
⇔ x + 6y = 375 (2)
Từ (1) và (2) ta có hệ phương trình:
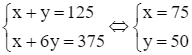
Vậy chiều dài là 75m và chiều rộng là 50m
Diện tích là: 75.50 = 3750 (m2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. h = S × 2 : a
B. h = S : 2 : a
C. h = S × 2 × a
D. h = a × S : 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập