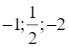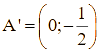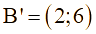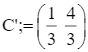Cho phương trình x2 – (2m – 1)x + 6 – 4m2 = 0.
Tìm m để phương trình có 2 nghiệm trái dấu sao cho x12 + x1 + x1x2 = 6x22 + 2x2.
Cho phương trình x2 – (2m – 1)x + 6 – 4m2 = 0.
Tìm m để phương trình có 2 nghiệm trái dấu sao cho x12 + x1 + x1x2 = 6x22 + 2x2.Quảng cáo
Trả lời:
Giải bởi Vietjack
Áp dụng hệ thức Vi-ét ta có: 
Vì x1 là nghiệm của phương trình nên ta có:
x12 – (2m – 1)x1 + 6 – 4m2 = 0
⇔ x12 + x1 + 6 – 4m2 = 2mx1
Mà 6 – 4m2 = x1x2 nên: x12 + x1 + x1x2 = 2mx1
⇔ 2mx1 = 6x22 + 2x2
⇔ mx1 = 3x22 + x2
Lại có: x1 = 2m – 1 – x2 (theo Vi-ét)
Suy ra: m(2m – 1 – x2) = 3x22 + x2
⇔ (m + x2)(2m – 3x2) – (m + x2) = 0
⇔ (m + x2)(2m – 3x2 – 1) = 0
⇔ 
+ Nếu x2 = -m thì x1 = 3m – 1
Khi đó: (3m – 1). (-m) = 6 – 4m2
⇔ m2 + m – 6 = 0
⇔ 
+ Nếu 
thì 
Khi đó: 
⇔ 4m2 – 4m + 1 = 27 – 18m2
⇔ 22m2 – 4m – 26 = 0
⇔ 
(loại)
Vậy m = -3 hoặc m = 2.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
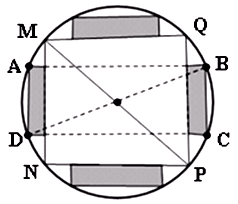
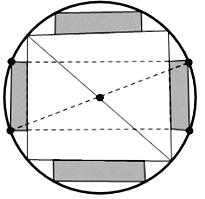
Gọi x, y lần lượt là chiều rộng và chiều dài của miếng phụ.
Diện tích sử dụng theo tiết diện ngang là S = SMNPQ + 4xy.
Cạnh hình vuông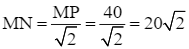 
(cm).
Suy ra 
(1)
Ta có:
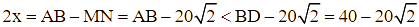
, suy ra:
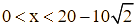
Lại có 
Suy ra 
, suy ra 
Thế vào (1):
Xét hàm số 
với 
có:
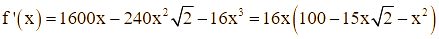
Ta có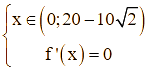 
nên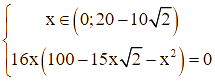 
Do đó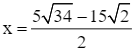 
.
Lời giải
Gọi I(x; y; z) là điểm thỏa mãn 
(*).
Ta có 
Khi đó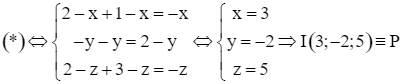 
Suy ra 
Suy ra IA2 = 14; IB2 = 50; IC2 = 12.
Ta có 
Khi đó 
= 0.
Hay 
Vậy 
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập