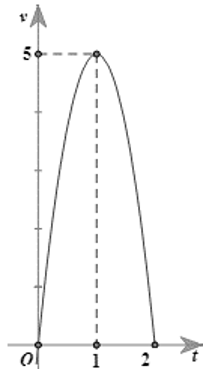
Một người chạy trong thời gian 1 giờ, vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần parabol với đỉnh \(I\left( {\frac{1}{2};{\rm{ }}8} \right)\) và trục đối xứng song song với trục tung như hình bên. Tính quảng đường \(s\) người đó chạy được trong khoảng thời gian \(45\) phút, kể từ khi chạy?
Trả lời:……………………………..
Một người chạy trong thời gian 1 giờ, vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần parabol với đỉnh \(I\left( {\frac{1}{2};{\rm{ }}8} \right)\) và trục đối xứng song song với trục tung như hình bên. Tính quảng đường \(s\) người đó chạy được trong khoảng thời gian \(45\) phút, kể từ khi chạy?

Trả lời:……………………………..
Câu hỏi trong đề: (Trả lời ngắn) 26 bài tập Tích phân (có lời giải) !!
Quảng cáo
Trả lời:
Đáp án: \(s = 4,5\) (km)
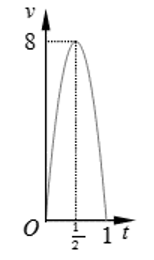
Gọi parabol là \(\left( P \right):y = a{x^2} + bx + c\). Từ hình vẽ ta có \(\left( P \right)\) đi qua \(O\left( {0;{\rm{ }}0} \right)\), \(A\left( {1;{\rm{ }}0} \right)\) và điểm \(I\left( {\frac{1}{2};{\rm{ }}8} \right)\).
Ta có hệ: \(\left\{ \begin{array}{l}c = 0\\a + b + c = 0\\\frac{a}{4} + \frac{b}{2} + c = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 32\\b = 32\\c = 0\end{array} \right.\).
Suy ra \(\left( P \right):y = - 32{x^2} + 32x\).
Vậy quảng đường người đó đi được là \[s = \int\limits_0^{\frac{3}{4}} {\left( { - 32{x^2} + 32x} \right){\rm{d}}x} = 4,5\](km).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Tại thời điểm \(t = 6\)vật đang chuyển động với vận tốc \({v_0}\) nên có \(v(6) = {v_0}\)\( \Leftrightarrow - \frac{5}{2}.6 + a\,\, = {v_0} \Leftrightarrow a\,\, = {v_0} + 15\), suy ra \(v(t) = - \frac{5}{2}t + {v_0} + 15\).
- Gọi \(k\)là thời điểm vật dừng hẳn, vậy ta có \(v(k) = 0 \Leftrightarrow k = \frac{2}{5}.\left( {{v_0} + 15} \right) \Leftrightarrow k = \frac{{2{v_0}}}{5} + 6\).
- Tổng quãng đường vật đi được là \[80 = 6.{v_0} + \int\limits_6^k {\left( { - \frac{5}{2}t + {v_0} + 15} \right)dt} \]
\[\begin{array}{l} \Leftrightarrow 80 = 6.{v_0} + \left. {\left( { - \frac{5}{4}{t^2} + {v_0}.t + 15t} \right)} \right|_6^k\\ \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}({k^2} - {6^2}) + {v_0}.(k - 6) + 15(k - 6)\\ \Leftrightarrow 80 = 6.{v_0} - \frac{5}{4}\left( {\frac{{4{{\left( {{v_0}} \right)}^2}}}{{25}} + \frac{{24{v_0}}}{5}} \right) + {v_0}.\frac{{2{v_0}}}{5} + 15.\frac{{2{v_0}}}{5}\\ \Leftrightarrow {\left( {{v_0}} \right)^2} + 36.{v_0} - 400 = 0\\ \Leftrightarrow {v_0} = 10\end{array}\]
Lời giải
\[\frac{{545}}{6}m\]
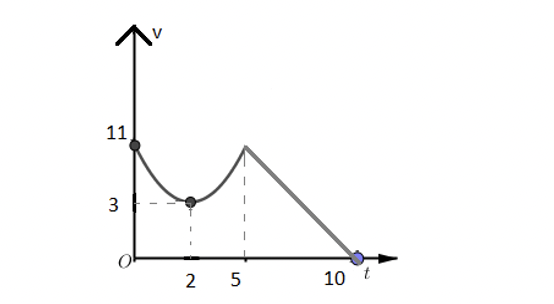
Gọi Parapol \[\left( P \right):y = a{x^2} + bx + c\] khi \[0 \le t \le 5\left( s \right)\]
Do \[\left( P \right):y = a{x^2} + bx + c\] đi qua \[I\left( {3;2} \right);A\left( {0;11} \right)\] nên
\[\left\{ \begin{array}{l}4a + 2b + c = 3\\c = 11\\4a + b = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 2\\b = - 8\\c = 11\end{array} \right..\]
Khi đó quãng đường vật di chuyển trong khoảng thời gian từ \[0 \le t \le 5\left( s \right)\] là \[S = \int\limits_0^5 {\left( {2{x^2} - 8x + 11} \right)dx = \frac{{115}}{3}} \left( m \right)\]
Ta có \[f\left( 5 \right) = 21\]
Gọi \[d:y = ax + b\] khi \[5 \le t \le 10\left( s \right)\] do \[d\] đi qua điểm \[B\left( {5;21} \right)\] và \[C\left( {10;0} \right)\] nên:
\[\left\{ \begin{array}{l}5a + b = 11\\10a + b = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - \frac{{21}}{5}\\b = 42\end{array} \right..\]
Khi đó quãng đường vật di chuyển trong khoảng thời gian từ \[5 \le t \le 10\left( s \right)\] là \[S = \int\limits_5^{10} {\left( { - \frac{{26}}{5}x + 52} \right)dx = \frac{{105}}{2}} \left( m \right)\]
Quãng đường đi được chất điểm trong thời gian \[0 \le t \le 10\left( s \right)\] là \[S = \frac{{115}}{3} + \frac{{105}}{2} = \frac{{545}}{6}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.