Ta đã biết công thức tính thể tích của khối cầu bán kính R là \(V = \frac{{4\pi {R^3}}}{3}\). Em hãy chứng minh công thức đó.

Xem lời giải

Câu hỏi trong đề: Các dạng bài tập Ứng dụng hình học của tích phân lớp 12 (có lời giải) !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Sau khi học xong bài, ta giải quyết bài toán này như sau:

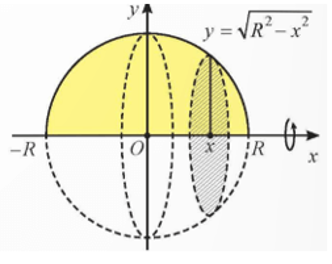
Ta đã biết công thức tính thể tích của khối cầu bán kính R là (ảnh 1)

Khối cầu có bán kính R là khối tròn xoay nhận được khi quay nửa hình tròn giới hạn bởi đồ thị hàm số \(y = \sqrt {{R^2} - {x^2}} ( - R \le x \le R)\) và trục Ox quanh trục Ox.

Từ đó thể tích khối cầu là: \(V = \pi \int_{ - R}^R {\left( {{R^2} - {x^2}} \right)} dx = \left. {\pi \left( {{R^2}x - \frac{{{x^3}}}{3}} \right)} \right|_{ - R}^R = \frac{{4\pi {R^3}}}{3}\)

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho khối chóp có chiều cao bằng h và diện tích bằng B. Chọ trục Ox vuông góc với mặt phẳng đáy tại điểm I sao cho gốc O trùng với đỉnh của khối chóp và có hướng xác định bởi véctơ \[\overrightarrow {OI} \] như hình bên. Khi OI = h. Một mặt phẳng (P) vuông góc với trục Ox tại x \[\left( {0 \le x \le h} \right)\], cắt khối chóp theo hình phẳng có diện tích S(x). Người ta chứng minh rằng \[S(x) = B\frac{{{x^2}}}{{{h^2}}}\]. Tính thể tích khối chóp đó.

Xem đáp án

Lời giải

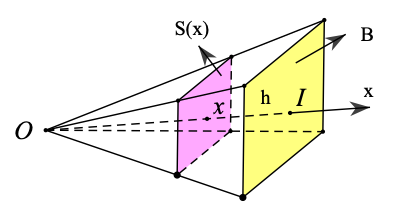
Thể tích khối chóp đó là: \(V = \int_0^h S (x){\rm{d}}x = \int_0^h B \frac{{{x^2}}}{{{h^2}}}\;{\rm{d}}x = \left. {B\frac{{{x^3}}}{{3{h^2}}}} \right|_0^h = B\frac{{{h^3}}}{{3{h^2}}} = \frac{{Bh}}{3}.\)

Câu 2

Cho khối chóp cụt đều tạo bởi khối chóp đỉnh S, diện tích hai đáy lần lượt là B, B’ và chiều cao h. Chọn trục Ox chứa đường cao của khối chóp và gốc O trùng với đỉnh S. Hai mặt phẳng đáy của khối chóp cụt đều lần lượt cắt Ox tại I và I’ . Đặt OI = b, OI’ = a (a< b). Một mặt phẳng (P) vuông góc với trục Ox tại x \[\left( {a \le x \le b} \right)\], cắt khối chóp cụt đều theo hình phẳng có diện tích S(x). Người ta chứng minh rằng \[S(x) = B\frac{{{x^2}}}{{{b^2}}}\]. Tính thể tích khối chóp cụt đó.

Xem đáp án

Lời giải

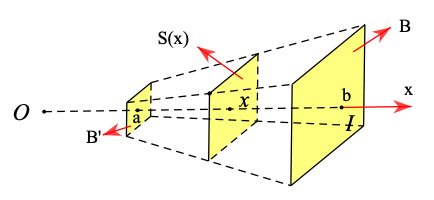
Thể tích khối chóp cụt đều đó là:

\(V = \int_a^b S (x)dx = \int_a^b B \frac{{{x^2}}}{{{b^2}}}dx = \left. {B\frac{{{x^3}}}{{3{b^2}}}} \right|_a^b = \frac{B}{{3{b^2}}}\left( {{b^3} - {a^3}} \right) = B \cdot \frac{{b - a}}{3} \cdot \frac{{{a^2} + ab + {b^2}}}{{{b^2}}} = \frac{{b - a}}{3} \cdot B\left( {\frac{{{a^2}}}{{{b^2}}} + \frac{a}{b} + 1} \right).\)

\({\rm{ Vi }}{B^\prime } = B\frac{{{a^2}}}{{{b^2}}}{\rm{ hay }}\frac{{{B^\prime }}}{B} = \frac{{{a^2}}}{{{b^2}}}{\rm{ và h}} = {\rm{b - a nên }}\)\(V = \frac{h}{3} \cdot B\left( {\frac{{{B^\prime }}}{B} + \sqrt {\frac{{{B^\prime }}}{B}} + 1} \right) = \frac{h}{3}\left( {B + \sqrt {B{B^\prime }} + {B^\prime }} \right).\)

Câu 3