Tốc độ tăng dân số của một thành phố trong một số năm được ước lượng bởi công thức \({{\rm{P}}^\prime }({\rm{t}}) = 20.{(1,106)^{\rm{t}}}\) với \(0 \le {\rm{t}} \le 7\), trong đó t là thời gian tính theo năm và $t=0$ ứng với đầu năm \(2015,{\rm{P}}({\rm{t}})\) là dân số của thành phố tính theo nghìn người. Cho biết dân số của thành phố đầu năm 2015 là 1008 nghìn người.

a) Tính dân số của thành phố ở thời điếm đầu năm 2020 (làm tròn đến nghìn người).

b) Tính tốc độ tăng dân số trung bình hằng năm của thành phố trong giai đoạn từ đằu năm 2015 đến đằu năm 2020 .

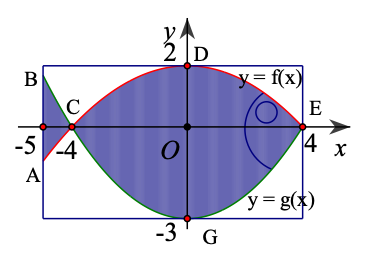
a) Giả sử parabol \(y = f(x)\) cho bời \(f(x) = a{x^2} + bx + c(a \ne 0)\). Do parabol \(y = f(x)\) đi qua điểm \(D(0;2)\) nên \(c = 2\), suy ra \(f(x) = a{x^2} + bx + 2(a \ne 0)\). Vì parabol \(y = f(x)\) đi qua các điểm \(C( - 4;0),E(4;0)\) nên ta có: \(\left\{ {\begin{array}{*{20}{l}}{16a - 4b + 2 = 0}\\{16a + 4b + 2 = 0.}\end{array}} \right.\)

Hệ phương trình trên có nghiệm là \(a =  - \frac{1}{8},b = 0\). Vậy \(f(x) =  - \frac{1}{8}{x^2} + 2\).

- Giả sử parabol \(y = g(x)\) cho bởi \(g(x) = {a_1}{x^2} + {b_1}x + {c_1}\left( {{a_1} \ne 0} \right)\). Do parabol \(y = g(x)\) đi qua điểm \(G(0; - 3)\) nên \({c_1} =  - 3\), suy ra \(g(x) = {a_1}{x^2} + {b_1}x - 3\left( {{a_1} \ne 0} \right)\). Vì parabol \(y = g(x)\) đi qua các điểm \(C( - 4;0),E(4;0)\) nên ta có: \(\left\{ {\begin{array}{*{20}{l}}{16{a_1} - 4{b_1} - 3 = 0}\\{16{a_1} + 4{b_1} - 3 = 0.}\end{array}} \right.\)

Hệ phương trình trên có nghiệm là \({a_1} = \frac{3}{{16}},{b_1} = 0\). Vậy \(g(x) = \frac{3}{{16}}{x^2} - 3\).

b) Diện tích của logo là: \(S = {S_1} + {S_2}\), trong đó \({S_1}\) là diện tích hình phẳng giới hạn bởi các parabol \(f(x) =  - \frac{1}{8}{x^2} + 2,g(x) = \frac{3}{{16}}{x^2} - 3\) và hai đường thẳng \(x =  - 5,x =  - 4\); \({S_2}\) là diện tích hình phẳng giới hạn bởi các parabol \(f(x) =  - \frac{1}{8}{x^2} + 2,g(x) = \frac{3}{{16}}{x^2} - 3\) và hai đường thẳng \(x =  - 4,x = 4\).

Do đó, ta có:

\(S = \int_{ - 5}^{ - 4} | f(x) - g(x)|{\rm{d}}x + \int_{ - 4}^4 | f(x) - g(x)|{\rm{d}}x\)

\( = \int_{ - 5}^{ - 4} {\left[ {\left( {\frac{3}{{16}}{x^2} - 3} \right) - \left( { - \frac{1}{8}{x^2} + 2} \right)} \right]} {\rm{d}}x + \int_{ - 4}^4 {\left[ {\left( { - \frac{1}{8}{x^2} + 2} \right) - \left( {\frac{3}{{16}}{x^2} - 3} \right)} \right]} {\rm{d}}x\)

\( = \int_{ - 5}^4 {\left( {\frac{5}{{16}}{x^2} - 5} \right)} {\rm{d}}x + \int_{ - 4}^4 {\left( { - \frac{5}{{16}}{x^2} + 5} \right)} {\rm{d}}x\)

\( = \left. {\frac{5}{{48}}{x^3}} \right|_{ - 5}^{ - 4} - \left. {5x} \right|_{ - 5}^{ - 4} - \left. {\frac{5}{{48}}{x^3}} \right|_{ - 4}^4 + \left. {5x} \right|_{ - 4}^4\)

\( = \frac{{305}}{{48}} - 5 - \frac{{640}}{{48}} + 40 = \frac{{1345}}{{48}}.\)

\(S = \frac{{1345}}{{48}}\left( {{\rm{d}}{{\rm{m}}^2}} \right).\)

c) Gọi \(t\) là lượng ánh sáng đi qua mỗi $\mathrm{dm}^2$ của logo. Suy ra lượng ánh sáng đi qua logo là \(\frac{{1345}}{{48}}t\). Mặt khác, diện tích của cửa sổ là \((8 + 1) \cdot (2 + 3) = 45\left( {{\rm{d}}{{\rm{m}}^2}} \right)\) và lượng ánh sáng đi qua mỗi \({\rm{d}}{{\rm{m}}^2}\) của phần cửa sổ nằm ngoài logo là 2t. Suy ra, lượng ánh sáng đi qua cửa sổ trược khi làm logo là \(45.2t = 90t\) và lượng ánh sáng đi qua phẩn cửa sổ nằm ngoài logo là: \(\left( {45 - \frac{{1345}}{{48}}} \right)2t = \frac{{815}}{{24}}t\)

Do đó, tổng lượng ánh sáng đi qua cửa sổ sau khi làm logo là: \(\frac{{1345}}{{48}}t + \frac{{815}}{{24}}t = \frac{{2975}}{{48}}t.\)

Tỉ số phần trăm của lượng ánh sáng đi qua cửa sổ sau khi làm logo so vởi lượng ánh sáng đi qua cửa sổ trược khi làm logo là:  \(\left( {\frac{{2975}}{{48}}t:90t} \right) \cdot 100\%  = \frac{{297500}}{{4320}}\%  \approx 68,9\% {\rm{. }}\)

Vậy lượng ánh sáng khi đi qua toàn bộ cửa sổ sau khi làm logo sẽ giảm đi xấp xỉ là: 100% - 68,9% = 31,1%