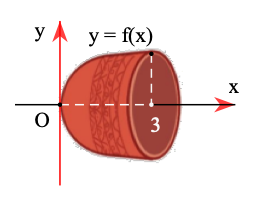
Cho tam giác OPM có cạnh OP nằm trên trục Ox. Giải sử \[\widehat {POM} = \alpha ,OM = l{\rm{ }}\left( {0 \le \alpha  \le \frac{\pi }{3};t > 0} \right)\]. Gọi N là khối nón tròn xoay thu được khi tam giác đó xuay quanh trục Ox. Tính thể tích khối nón N theo \[l\].

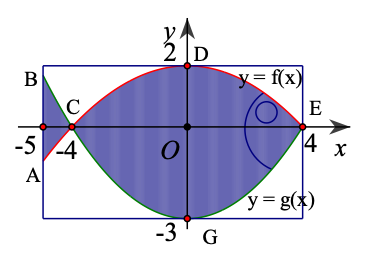
a) Giả sử parabol \(y = f(x)\) cho bời \(f(x) = a{x^2} + bx + c(a \ne 0)\). Do parabol \(y = f(x)\) đi qua điểm \(D(0;2)\) nên \(c = 2\), suy ra \(f(x) = a{x^2} + bx + 2(a \ne 0)\). Vì parabol \(y = f(x)\) đi qua các điểm \(C( - 4;0),E(4;0)\) nên ta có: \(\left\{ {\begin{array}{*{20}{l}}{16a - 4b + 2 = 0}\\{16a + 4b + 2 = 0.}\end{array}} \right.\)

Hệ phương trình trên có nghiệm là \(a =  - \frac{1}{8},b = 0\). Vậy \(f(x) =  - \frac{1}{8}{x^2} + 2\).

- Giả sử parabol \(y = g(x)\) cho bởi \(g(x) = {a_1}{x^2} + {b_1}x + {c_1}\left( {{a_1} \ne 0} \right)\). Do parabol \(y = g(x)\) đi qua điểm \(G(0; - 3)\) nên \({c_1} =  - 3\), suy ra \(g(x) = {a_1}{x^2} + {b_1}x - 3\left( {{a_1} \ne 0} \right)\). Vì parabol \(y = g(x)\) đi qua các điểm \(C( - 4;0),E(4;0)\) nên ta có: \(\left\{ {\begin{array}{*{20}{l}}{16{a_1} - 4{b_1} - 3 = 0}\\{16{a_1} + 4{b_1} - 3 = 0.}\end{array}} \right.\)

Hệ phương trình trên có nghiệm là \({a_1} = \frac{3}{{16}},{b_1} = 0\). Vậy \(g(x) = \frac{3}{{16}}{x^2} - 3\).

b) Diện tích của logo là: \(S = {S_1} + {S_2}\), trong đó \({S_1}\) là diện tích hình phẳng giới hạn bởi các parabol \(f(x) =  - \frac{1}{8}{x^2} + 2,g(x) = \frac{3}{{16}}{x^2} - 3\) và hai đường thẳng \(x =  - 5,x =  - 4\); \({S_2}\) là diện tích hình phẳng giới hạn bởi các parabol \(f(x) =  - \frac{1}{8}{x^2} + 2,g(x) = \frac{3}{{16}}{x^2} - 3\) và hai đường thẳng \(x =  - 4,x = 4\).

Do đó, ta có:

\(S = \int_{ - 5}^{ - 4} | f(x) - g(x)|{\rm{d}}x + \int_{ - 4}^4 | f(x) - g(x)|{\rm{d}}x\)

\( = \int_{ - 5}^{ - 4} {\left[ {\left( {\frac{3}{{16}}{x^2} - 3} \right) - \left( { - \frac{1}{8}{x^2} + 2} \right)} \right]} {\rm{d}}x + \int_{ - 4}^4 {\left[ {\left( { - \frac{1}{8}{x^2} + 2} \right) - \left( {\frac{3}{{16}}{x^2} - 3} \right)} \right]} {\rm{d}}x\)

\( = \int_{ - 5}^4 {\left( {\frac{5}{{16}}{x^2} - 5} \right)} {\rm{d}}x + \int_{ - 4}^4 {\left( { - \frac{5}{{16}}{x^2} + 5} \right)} {\rm{d}}x\)

\( = \left. {\frac{5}{{48}}{x^3}} \right|_{ - 5}^{ - 4} - \left. {5x} \right|_{ - 5}^{ - 4} - \left. {\frac{5}{{48}}{x^3}} \right|_{ - 4}^4 + \left. {5x} \right|_{ - 4}^4\)

\( = \frac{{305}}{{48}} - 5 - \frac{{640}}{{48}} + 40 = \frac{{1345}}{{48}}.\)

\(S = \frac{{1345}}{{48}}\left( {{\rm{d}}{{\rm{m}}^2}} \right).\)

c) Gọi \(t\) là lượng ánh sáng đi qua mỗi $\mathrm{dm}^2$ của logo. Suy ra lượng ánh sáng đi qua logo là \(\frac{{1345}}{{48}}t\). Mặt khác, diện tích của cửa sổ là \((8 + 1) \cdot (2 + 3) = 45\left( {{\rm{d}}{{\rm{m}}^2}} \right)\) và lượng ánh sáng đi qua mỗi \({\rm{d}}{{\rm{m}}^2}\) của phần cửa sổ nằm ngoài logo là 2t. Suy ra, lượng ánh sáng đi qua cửa sổ trược khi làm logo là \(45.2t = 90t\) và lượng ánh sáng đi qua phẩn cửa sổ nằm ngoài logo là: \(\left( {45 - \frac{{1345}}{{48}}} \right)2t = \frac{{815}}{{24}}t\)

Do đó, tổng lượng ánh sáng đi qua cửa sổ sau khi làm logo là: \(\frac{{1345}}{{48}}t + \frac{{815}}{{24}}t = \frac{{2975}}{{48}}t.\)

Tỉ số phần trăm của lượng ánh sáng đi qua cửa sổ sau khi làm logo so vởi lượng ánh sáng đi qua cửa sổ trược khi làm logo là:  \(\left( {\frac{{2975}}{{48}}t:90t} \right) \cdot 100\%  = \frac{{297500}}{{4320}}\%  \approx 68,9\% {\rm{. }}\)

Vậy lượng ánh sáng khi đi qua toàn bộ cửa sổ sau khi làm logo sẽ giảm đi xấp xỉ là: 100% - 68,9% = 31,1%